|
Biogeme: Python Library
2.5
|
Class performing numerical integration relying on the Gauss-Hermite quadrature to compute
![\[ \int_{-\infty}^{+\infty} f(\omega) d\omega. \]](form_14.png)
. More...
Public Member Functions | |
| def | __init__ (self, term, v) |
| def | getExpression (self) |
 Public Member Functions inherited from bio_expression.Expression | |
| def | __init__ (self) |
| Constructor. | |
| def | getExpression (self) |
| def | getID (self) |
| def | __str__ (self) |
| def | __neg__ (self) |
| def | __add__ (self, expression) |
| def | __radd__ (self, expression) |
| def | __sub__ (self, expression) |
| def | __rsub__ (self, expression) |
| def | __mul__ (self, expression) |
| def | __rmul__ (self, expression) |
| def | __div__ (self, expression) |
| def | __rdiv__ (self, expression) |
| def | __truediv__ (self, expression) |
| Support for Python version 3.x. More... | |
| def | __rtruediv__ (self, expression) |
| Support for Python version 3.x. More... | |
| def | __mod__ (self, expression) |
| def | __pow__ (self, expression) |
| def | __rpow__ (self, expression) |
| def | __and__ (self, expression) |
| def | __or__ (self, expression) |
| def | __eq__ (self, expression) |
| def | __ne__ (self, expression) |
| def | __le__ (self, expression) |
| def | __ge__ (self, expression) |
| def | __lt__ (self, expression) |
| def | __gt__ (self, expression) |
Public Attributes | |
| function | |
| variable | |
| operatorIndex | |
| Public Attributes inherited from bio_expression.Expression | |
| operatorIndex | |
Class performing numerical integration relying on the Gauss-Hermite quadrature to compute
.
As an example, the computation of a normal mixture of logit models is performed using the following syntax, where condprob is the conditional (logit) choice probability:
Comments:
![\[ \int_{-\infty}^{+\infty} e^{-\omega^2} f(\omega) d\omega. \]](form_15.png)
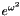before applying the Gauss-Hermite algorithm. This is transparent for the user.It is usually more accurate to compute an integral using a quadrature procedure. However, it should be used only in the presence of few (one or two) random variables. The same integral can be computed using Monte-Carlo integration using the following syntax:
Definition at line 783 of file bio_expression.py.
| def bio_expression.Integrate.__init__ | ( | self, | |
| term, | |||
| v | |||
| ) |
| term | any valid bio_expression representing the expression to integrate |
| v | name of the integration variable, previously defined using a bioExpression::RandomVariable statement. |
Definition at line 786 of file bio_expression.py.
