|
Biogeme: Python Library
2.5
|
|
Biogeme: Python Library
2.5
|
Functions | |
| def | distributions.normalpdf (x, mu=0.0, s=1.0) |
| Normal pdf. More... | |
| def | distributions.lognormalpdf (x, mu, s) |
| Log normal pdf. More... | |
| def | distributions.uniformpdf (x, a=-1, b=1.0) |
| Uniform pdf. More... | |
| def | distributions.triangularpdf (x, a=-1.0, b=1.0, c=0.0) |
| Triangular pdf. More... | |
| def | distributions.logisticcdf (x, mu=0.0, s=1.0) |
| Logistic CDF. More... | |
| def distributions.logisticcdf | ( | x, | |
mu = 0.0, |
|||
s = 1.0 |
|||
| ) |
Logistic CDF.
Cumulative distribution function of a logistic distribution
![\[ f(x;\mu,\sigma) = \frac{1}{1+\exp\left(-\frac{x-\mu}{\sigma} \right)} \]](form_43.png)
| x | argument of the pdf |
| mu | location parameter 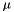 (Default: 0) (Default: 0) |
| s | scale parameter 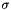 (Default: 1) (Default: 1) |
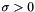 , but it is not verified by the code.
, but it is not verified by the code. Definition at line 74 of file distributions.py.
| def distributions.lognormalpdf | ( | x, | |
| mu, | |||
| s | |||
| ) |
Log normal pdf.
Probability density function of a log normal distribution
![\[ f(x;\mu,\sigma) = \frac{1}{x\sigma \sqrt{2\pi}} \exp{-\frac{(\ln x-\mu)^2}{2\sigma^2}} \]](form_36.png)
| x | argument of the pdf |
| mu | location parameter 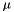 (Default: 0) (Default: 0) |
| s | scale parameter 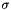 (Default: 1) (Default: 1) |
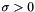 , but it is not verified by the code.
, but it is not verified by the code. Definition at line 32 of file distributions.py.
| def distributions.normalpdf | ( | x, | |
mu = 0.0, |
|||
s = 1.0 |
|||
| ) |
Normal pdf.
Probability density function of a normal distribution
![\[ f(x;\mu,\sigma) = \frac{1}{\sigma \sqrt{2\pi}} \exp{-\frac{(x-\mu)^2}{2\sigma^2}} \]](form_33.png)
| x | argument of the pdf |
| mu | location parameter 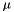 (Default: 0) (Default: 0) |
| s | scale parameter 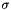 (Default: 1) (Default: 1) |
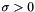 , but it is not verified by the code.
, but it is not verified by the code. Definition at line 15 of file distributions.py.
| def distributions.triangularpdf | ( | x, | |
a = -1.0, |
|||
b = 1.0, |
|||
c = 0.0 |
|||
| ) |
Triangular pdf.
Probability density function of a triangular distribution
![\[ f(x;a,b,c) = \left\{ \begin{array}{ll} 0 & \text{if } x < a \\\frac{2(x-a)}{(b-a)(c-a)} & \text{if } a \leq x < c \\\frac{2(b-x)}{(b-a)(b-c)} & \text{if } c \leq x < b \\0 & \text{if } x \geq b.\end{array} \right.\]](form_40.png)
| x | argument of the pdf |
| a | lower bound 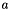 of the distribution (Default: -1) of the distribution (Default: -1) |
| b | upper bound 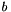 of the distribution (Default: 1) of the distribution (Default: 1) |
| c | mode 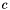 of the distribution (Default: 0) of the distribution (Default: 0) |
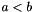 , and
, and 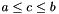 , but it is not verified by the code.
, but it is not verified by the code. Definition at line 62 of file distributions.py.
| def distributions.uniformpdf | ( | x, | |
a = -1, |
|||
b = 1.0 |
|||
| ) |
Uniform pdf.
Probability density function of a uniform distribution
![\[ f(x;a,b) = \left\{ \begin{array}{ll} \frac{1}{b-a} & \text{for } x \in [a,b] \\ 0 & \text{otherwise}\end{array} \right.\]](form_37.png)
| x | argument of the pdf |
| a | lower bound 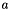 of the distribution (Default: -1) of the distribution (Default: -1) |
| b | upper bound 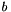 of the distribution (Default: 1) of the distribution (Default: 1) |
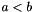 , but it is not verified by the code.
, but it is not verified by the code. Definition at line 49 of file distributions.py.