|
Biogeme: Python Library
2.5
|
|
Biogeme: Python Library
2.5
|
Functions | |
| def | cnl.cnl_avail (V, availability, nests, choice) |
| Implements the cross-nested logit model as a MEV model. More... | |
| def | cnl.logcnl_avail (V, availability, nests, choice) |
| Implements the log of the cross-nested logit model as a MEV model. More... | |
| def | cnl.cnlmu (V, availability, nests, choice, bmu) |
| Implements the cross-nested logit model as a MEV model with the homogeneity parameters is explicitly involved. More... | |
| def | cnl.logcnlmu (V, availability, nests, choice, bmu) |
| Implements the log of the cross-nested logit model as a MEV model with the homogeneity parameters is explicitly involved. More... | |
| def | logit.logit_av_scale (V, availability, choice, group, scale) |
| Compute the logit choice probability with utilities scaled according to the group. More... | |
| def | logit.logit (V, choice) |
| Compute the logit choice probability, where all alternatives are available. More... | |
| def | logit.logit_scale (V, choice, group, scale) |
| Compute the logit choice probability with utilities scaled according to the group. More... | |
| def | mev.mev (V, Gi, av, choice) |
| Choice probability for a MEV model. More... | |
| def | mev.logmev (V, Gi, av, choice) |
| Log of the choice probability for a MEV model. More... | |
| def | mev.mev_selectionBias (V, Gi, av, correction, choice) |
| Choice probability for a MEV model, including the correction for endogenous sampling as proposed by Bierlaire, Bolduc and McFadden (2008). More... | |
| def | mev.logmev_selectionBias (V, Gi, av, correction, choice) |
| Log of choice probability for a MEV model, including the correction for endogenous sampling as proposed by Bierlaire, Bolduc and McFadden (2008). More... | |
| def | nested.getMevForNested (V, availability, nests) |
| Implements the MEV generating function for the nested logit model. More... | |
| def | nested.nested (V, availability, nests, choice) |
| Implements the nested logit model as a MEV model. More... | |
| def | nested.lognested (V, availability, nests, choice) |
| Implements the log of a nested logit model as a MEV model. More... | |
| def | nested.nestedMevMu (V, availability, nests, choice, mu) |
| Implements the nested logit model as a MEV model, where mu is also a parameter, if the user wants to test different normalization schemes. More... | |
| def | nested.lognestedMevMu (V, availability, nests, choice, mu) |
| Implements the log of the nested logit model as a MEV model, where mu is also a parameter, if the user wants to test different normalization schemes. More... | |
| def cnl.cnl_avail | ( | V, | |
| availability, | |||
| nests, | |||
| choice | |||
| ) |
Implements the cross-nested logit model as a MEV model.
| V | A dictionary mapping each alternative id with the expression of the utility function. |
| availability | A dictionary mapping each alternative id with its availability condition. |
| nests | A tuple containing as many items as nests. Each item is also a tuple containing two items:
|
| def cnl.cnlmu | ( | V, | |
| availability, | |||
| nests, | |||
| choice, | |||
| bmu | |||
| ) |
Implements the cross-nested logit model as a MEV model with the homogeneity parameters is explicitly involved.
| V | A dictionary mapping each alternative id with the expression of the utility function. |
| availability | A dictionary mapping each alternative id with its availability condition. |
| nests | A tuple containing as many items as nests. Each item is also a tuple containing two items:
|
| bmu | Homogeneity parameter 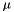 . . |
| def nested.getMevForNested | ( | V, | |
| availability, | |||
| nests | |||
| ) |
Implements the MEV generating function for the nested logit model.
| V | A dictionary mapping each alternative id with the expression of the utility function. |
| availability | A dictionary mapping each alternative id with its availability condition. |
| nests | A tuple containing as many items as nests. Each item is also a tuple containing two items:
|
![\[ \frac{\partial G}{\partial y_i}(e^{V_1},\ldots,e^{V_J}) = e^{(\mu_m-1)V_i} \left(\sum_{i=1}^{J_m} e^{\mu_m V_i}\right)^{\frac{1}{\mu_m}-1} \]](form_75.png)
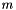 is the (only) nest containing alternative
is the (only) nest containing alternative 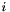 , and
, and 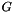 is the MEV generating function.
is the MEV generating function. | def cnl.logcnl_avail | ( | V, | |
| availability, | |||
| nests, | |||
| choice | |||
| ) |
Implements the log of the cross-nested logit model as a MEV model.
| V | A dictionary mapping each alternative id with the expression of the utility function. |
| availability | A dictionary mapping each alternative id with its availability condition. |
| nests | A tuple containing as many items as nests. Each item is also a tuple containing two items:
|
| def cnl.logcnlmu | ( | V, | |
| availability, | |||
| nests, | |||
| choice, | |||
| bmu | |||
| ) |
Implements the log of the cross-nested logit model as a MEV model with the homogeneity parameters is explicitly involved.
| V | A dictionary mapping each alternative id with the expression of the utility function. |
| availability | A dictionary mapping each alternative id with its availability condition. |
| nests | A tuple containing as many items as nests. Each item is also a tuple containing two items:
|
| bmu | Homogeneity parameter 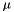 . . |
| def logit.logit | ( | V, | |
| choice | |||
| ) |
Compute the logit choice probability, where all alternatives are available.
| V | A dictionary mapping each alternative id with the expression of the utility function. |
| choice | expression producing the id of the chosen alternative. |
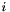 and individual in group
and individual in group 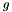 :
:
![\[ \frac{e^{V_i}}{\sum_j e^{V_j}}\]](form_58.png)
| def logit.logit_av_scale | ( | V, | |
| availability, | |||
| choice, | |||
| group, | |||
| scale | |||
| ) |
Compute the logit choice probability with utilities scaled according to the group.
| V | A dictionary mapping each alternative id with the expression of the utility function. |
| availability | A dictionary mapping each alternative id with its availability condition. |
| choice | expression producing the id of the chosen alternative. |
| group | id of the group, or market segment. |
| scale | A dictionary mapping each group id with the expression providing the corresponding scale. |
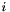 and individual in group
and individual in group 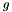 :
:
![\[ \frac{e^{\mu_g V_i}}{\sum_j a_j e^{\mu_g V_j}}\]](form_54.png)
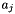 is 1 if alternative
is 1 if alternative 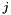 is available, 0 otherwise, and
is available, 0 otherwise, and 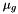 is the scale parameter associated with group
is the scale parameter associated with group 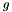 .
. | def logit.logit_scale | ( | V, | |
| choice, | |||
| group, | |||
| scale | |||
| ) |
Compute the logit choice probability with utilities scaled according to the group.
| V | A dictionary mapping each alternative id with the expression of the utility function. |
| choice | expression producing the id of the chosen alternative. |
| group | id of the group, or market segment. |
| scale | A dictionary mapping each group id with the expression providing the corresponding scale. |
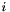 and individual in group
and individual in group 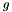 :
:
![\[ \frac{e^{\mu_g V_i}}{\sum_j e^{\mu_g V_j}}\]](form_59.png)
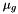 is the scale parameter associated with group
is the scale parameter associated with group 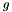 .
. | def mev.logmev | ( | V, | |
| Gi, | |||
| av, | |||
| choice | |||
| ) |
Log of the choice probability for a MEV model.
| V | A dictionary mapping each alternative id with the expression of the utility function. |
| Gi | A dictionary mapping each alternative id with the function
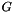 is the MEV generating function. If an alternative is the MEV generating function. If an alternative 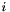 is not available, then is not available, then 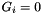 . . |
| av | A dictionary mapping each alternative id with its availability condition. |
| choice | Expression producing the id of the chosen alternative. |
![\[ V_i + \ln G_i(e^{V_1},\ldots,e^{V_J}) - \log\left(\sum_j e^{V_j + \ln G_j(e^{V_1},\ldots,e^{V_J})}\right) \]](form_74.png)
| def mev.logmev_selectionBias | ( | V, | |
| Gi, | |||
| av, | |||
| correction, | |||
| choice | |||
| ) |
Log of choice probability for a MEV model, including the correction for endogenous sampling as proposed by Bierlaire, Bolduc and McFadden (2008).
| V | A dictionary mapping each alternative id with the expression of the utility function. |
| Gi | A dictionary mapping each alternative id with the function
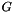 is the MEV generating function. is the MEV generating function. |
| av | A dictionary mapping each alternative id with its availability condition. |
| correction | A dictionary mapping each alternative id with the expression of the correction. Typically, it is a value, or a parameter to be estimated. |
| choice | Expression producing the id of the chosen alternative. |
![\[ V_i + \ln G_i(e^{V_1},\ldots,e^{V_J}) - \log\left(\sum_j e^{V_j + \ln G_j(e^{V_1},\ldots,e^{V_J})}\right) \]](form_74.png)
| def nested.lognested | ( | V, | |
| availability, | |||
| nests, | |||
| choice | |||
| ) |
Implements the log of a nested logit model as a MEV model.
| V | A dictionary mapping each alternative id with the expression of the utility function. |
| availability | A dictionary mapping each alternative id with its availability condition. |
| nests | A tuple containing as many items as nests. Each item is also a tuple containing two items:
|
| choice | expression producing the id of the chosen alternative. |
| def nested.lognestedMevMu | ( | V, | |
| availability, | |||
| nests, | |||
| choice, | |||
| mu | |||
| ) |
Implements the log of the nested logit model as a MEV model, where mu is also a parameter, if the user wants to test different normalization schemes.
| V | A dictionary mapping each alternative id with the expression of the utility function. |
| availability | A dictionary mapping each alternative id with its availability condition. |
| nests | A tuple containing as many items as nests. Each item is also a tuple containing two items:
|
| choice | expression producing the id of the chosen alternative. |
| mu | expression producing the value of the top-level scale parameter. |
![\[ \frac{\partial G}{\partial y_i}(e^{V_1},\ldots,e^{V_J}) = \mu e^{(\mu_m-1)V_i} \left(\sum_{i=1}^{J_m} e^{\mu_m V_i}\right)^{\frac{\mu}{\mu_m}-1} \]](form_76.png)
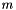 is the (only) nest containing alternative
is the (only) nest containing alternative 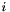 , and
, and 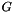 is the MEV generating function.
is the MEV generating function. | def mev.mev | ( | V, | |
| Gi, | |||
| av, | |||
| choice | |||
| ) |
Choice probability for a MEV model.
| V | A dictionary mapping each alternative id with the expression of the utility function. |
| Gi | A dictionary mapping each alternative id with the function
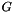 is the MEV generating function. If an alternative is the MEV generating function. If an alternative 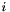 is not available, then is not available, then 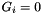 . . |
| av | A dictionary mapping each alternative id with its availability condition. |
| choice | Expression producing the id of the chosen alternative. |
![\[ \frac{e^{V_i + \ln G_i(e^{V_1},\ldots,e^{V_J})}}{\sum_j e^{V_j + \ln G_j(e^{V_1},\ldots,e^{V_J})}} \]](form_73.png)
| def mev.mev_selectionBias | ( | V, | |
| Gi, | |||
| av, | |||
| correction, | |||
| choice | |||
| ) |
Choice probability for a MEV model, including the correction for endogenous sampling as proposed by Bierlaire, Bolduc and McFadden (2008).
| V | A dictionary mapping each alternative id with the expression of the utility function. |
| Gi | A dictionary mapping each alternative id with the function
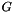 is the MEV generating function. is the MEV generating function. |
| av | A dictionary mapping each alternative id with its availability condition. |
| correction | A dictionary mapping each alternative id with the expression of the correction. Typically, it is a value, or a parameter to be estimated. |
| choice | Expression producing the id of the chosen alternative. |
![\[ \frac{e^{V_i + \ln G_i(e^{V_1},\ldots,e^{V_J})}}{\sum_j e^{V_j + \ln G_j(e^{V_1},\ldots,e^{V_J})}} \]](form_73.png)
| def nested.nested | ( | V, | |
| availability, | |||
| nests, | |||
| choice | |||
| ) |
Implements the nested logit model as a MEV model.
| V | A dictionary mapping each alternative id with the expression of the utility function. |
| availability | A dictionary mapping each alternative id with its availability condition. |
| nests | A tuple containing as many items as nests. Each item is also a tuple containing two items:
|
| choice | expression producing the id of the chosen alternative. |
| def nested.nestedMevMu | ( | V, | |
| availability, | |||
| nests, | |||
| choice, | |||
| mu | |||
| ) |
Implements the nested logit model as a MEV model, where mu is also a parameter, if the user wants to test different normalization schemes.
| V | A dictionary mapping each alternative id with the expression of the utility function. |
| availability | A dictionary mapping each alternative id with its availability condition. |
| nests | A tuple containing as many items as nests. Each item is also a tuple containing two items:
|
| choice | expression producing the id of the chosen alternative. |
| mu | expression producing the value of the top-level scale parameter. |
![\[ \frac{\partial G}{\partial y_i}(e^{V_1},\ldots,e^{V_J}) = \mu e^{(\mu_m-1)V_i} \left(\sum_{i=1}^{J_m} e^{\mu_m V_i}\right)^{\frac{\mu}{\mu_m}-1} \]](form_76.png)
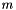 is the (only) nest containing alternative
is the (only) nest containing alternative 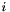 , and
, and 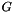 is the MEV generating function.
is the MEV generating function.