|
Biogeme: Python Library
2.5
|
|
Biogeme: Python Library
2.5
|
Fonctions for transformed Legendre polynomials, orthonormal on [0,1]:
![\[ L_n(x) = \frac{\sqrt{4n^2-1}}{n}(2x-1)L_{n-1}(x)-\frac{(n-1)\sqrt{2n+1}}{n \sqrt{2n-3}} L_{n-2}(x), \]](form_44.png)
with 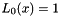 ,
, 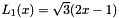 and
and 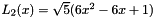 .
More...
.
More...
Go to the source code of this file.
Functions | |
| def | legendre.legendre00 (x) |
| Implements the transformed Legendre polynomials of degree 0
. More... | |
| def | legendre.legendre01 (x) |
| Implements the transformed Legendre polynomials of degree 1
. More... | |
| def | legendre.legendre02 (x) |
| Implements the transformed Legendre polynomials of degree 2
. More... | |
| def | legendre.legendre03 (x) |
| Implements the transformed Legendre polynomials of degree 3
. More... | |
| def | legendre.legendre04 (x) |
| Implements the transformed Legendre polynomials of degree 4. More... | |
| def | legendre.legendre05 (x) |
| Implements the transformed Legendre polynomials of degree 5. More... | |
| def | legendre.legendre06 (x) |
| Implements the transformed Legendre polynomials of degree 6. More... | |
| def | legendre.legendre07 (x) |
| Implements the transformed Legendre polynomials of degree 7. More... | |
Fonctions for transformed Legendre polynomials, orthonormal on [0,1]:
![\[ L_n(x) = \frac{\sqrt{4n^2-1}}{n}(2x-1)L_{n-1}(x)-\frac{(n-1)\sqrt{2n+1}}{n \sqrt{2n-3}} L_{n-2}(x), \]](form_44.png)
with 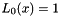 ,
, 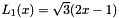 and
and 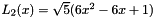 .
.
See [1].
Definition in file legendre.py.