Algorithm 18.2: Interior point algorithm with restricted steps. More...
Go to the source code of this file.
Functions | |
| function | restrictedSteps (in A, in b, in c, in x0, in lambda0, in mu0, in eps, in theta) |
| Applies the interior point algorithm with restricted steps to solve
subject to
and
. More... | |
Detailed Description
Algorithm 18.2: Interior point algorithm with restricted steps.
Implementation of algorithm 18.2 of [1]
- Note
- Tested with run1807restrictedSteps.m
- Date
- Mon Mar 23 10:59:13 2015
Definition in file restrictedSteps.m.
Function Documentation
◆ restrictedSteps()
| function restrictedSteps | ( | in | A, |
| in | b, | ||
| in | c, | ||
| in | x0, | ||
| in | lambda0, | ||
| in | mu0, | ||
| in | eps, | ||
| in | theta | ||
| ) |
Applies the interior point algorithm with restricted steps to solve
![\[\min_x c^Tx \]](form_79.png)
subject to
![\[Ax = b\]](form_80.png)
and
![\[ x \geq 0 \]](form_72.png)
.
- Parameters
-
A the constraint matrix b the constraint right hand side c the cost vector for the objective function x0 starting primal point (nx1) lambda0 starting dual point for equality constraints (mx1) mu0 starting dual point for inequality constraints (nx1) eps algorithm stops if 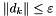 .
. theta parameter such that 0 <= theta <= 1 (default: 0.4) maxiter maximum number of iterations (default: 100)
- Returns
- [x,lambda,mu]
- x: primal solution
- lambda: dual solution for equality constraints
- mu: dual solution for inequality constraints