Algorithm 18.3: Predictor-corrector interior point algorithm. More...

Functions
function	predictorCorrector (in A, in b, in c, in x0, in lambda0, in mu0, in eps, in thetapred)
	Applies the predictor-corrector interior point algorithm to solve $\min_x c^Tx$ subject to $Ax = b$ and $x \geq 0$ . More...

Detailed Description

Algorithm 18.3: Predictor-corrector interior point algorithm.

Implementation of algorithm 18.3 of [1]

Function Documentation

function predictorCorrector	(	in	A,
		in	b,
		in	c,
		in	x0,
		in	lambda0,
		in	mu0,
		in	eps,
		in	thetapred
	)

Applies the predictor-corrector interior point algorithm to solve

$\min_x c^Tx$

subject to

$Ax = b$

and

$x \geq 0$

.

Parameters

A	the constraint matrix
b	the constraint right hand side
c	the cost vector for the objective function
x0	starting primal point (nx1)
lambda0	starting dual point for equality constraints (mx1)
mu0	starting dual point for inequality constraints (nx1)
eps	algorithm stops if 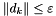$\\|d_k\\| \leq \varepsilon$ .
thetapred	parameter such that 0 <= theta <= 1 (default: 0.5)
thetacorr	parameter such that 0 <= theta <= 1 (default: 0.25)
maxiter	maximum number of iterations (default: 100)

Returns: [x,lambda,mu]; x: primal solution; lambda: dual solution for equality constraints; mu: dual solution for inequality constraints