Algorithm 8.1: Newton's method with finite differences, one variable. More...
Go to the source code of this file.
Functions | |
| function | newtonFinDiffOneVariable (in obj, in x0, in eps, in tau, in maxiter) |
Applies Newton's algorithm with finite differences to solve 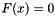 where where 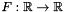 . More... . More... | |
Detailed Description
Algorithm 8.1: Newton's method with finite differences, one variable.
Implementation of algorithm 8.1 of [1]
- Date
- Thu Mar 19 09:44:05 2015
Definition in file newtonFinDiffOneVariable.m.
Function Documentation
◆ newtonFinDiffOneVariable()
| function newtonFinDiffOneVariable | ( | in | obj, |
| in | x0, | ||
| in | eps, | ||
| in | tau, | ||
| in | maxiter | ||
| ) |
Applies Newton's algorithm with finite differences to solve 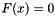 where
where 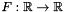 .
.
- Note
- Tested with run0703df.m
- Parameters
-
obj the name of the Octave function defining F(x) x0 the starting point eps algorithm stops if 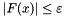 .
. tau step for the finite difference approximation maxiter maximum number of iterations (Default: 100)
- Returns
- root of the function