The package PythonBiogeme (biogeme.epfl.ch) is designed to estimate the parameters of various models using maximum likelihood estimation. It is particularly designed for discrete choice models. In this document, we investigate some aspects related to Monte-Carlo integration, which is particularly useful when estimating mixtures choice models, as well as choice models with latent variables. We assume that the reader is already familiar with discrete choice models, with PythonBiogeme, and with simulation methods, although a short summary is provided. This document has been written using PythonBiogeme 2.4, but should remain valid for future versions.

1 Monte-Carlo integration

Monte-Carlo integration consists in approximating an integral with the sum of a large number of terms. It comes from the definition of the expectation of a continuous random variable. Consider the random variable X with probability density function (pdf) f_X(x). Assuming that X can take any value in the interval [a,b], where a ∈ℝ ∪ {-∞} and b ∈ℝ ∪ {+∞}, the expected value of X is given by

(1)

Also, if g : ℝ → ℝ is a function, then

(2)

The expectation of a random variable can be approximated using simulation. The idea is simple: generate a sample of realizations of X, that is generate R draws x_r, r = 1,…,R from X, and calculate the sample mean:

(3)

Putting (2) and (3) together, we obtain an approximation to the integral:

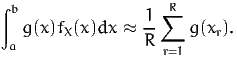(4)

Also, we have

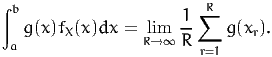(5)

Therefore, the procedure to calculate the following integral

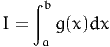(6)

is the following

1. Select a random variable X such that you can generate realizations of X, and such that the pdf f_X is known;
2. Generate R draws x_r, r = 1,…,R from X;
3. Calculate

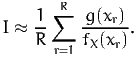   (7)

In order to obtain an estimate of the approximation error, we must calculate the variance the random variable. The sample variance is an unbiased estimate of the true variance:

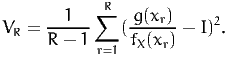(8)

Alternatively as

(9)

the variance can be approximated by simulation as well:

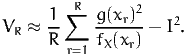(10)

Note that, for the values of R that we are using in this document, dividing by R or by R - 1 does not make much difference in practice. The approximation error is then estimated as

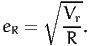(11)

We refer the reader to Ross (2012) for a comprehensive introduction to simulation methods.

2 Uniform draws

There are many algorithms to draw from various distributions. All of them require at some point draws from the uniform distribution. There are several techniques that generate such uniform draws. In PythonBiogeme, one of them must be selected by setting the parameter RandomDistribution.

Each programming language provides a routine to draw a random number between 0 and 1. Such routines are deterministic, but the sequences of numbers that they generate share many properties with sequences of random numbers. Therefore, they are often called “pseudo random numbers”.

Researchers have proposed to use other types of sequences to perform Monte-Carlo integration, called “quasi-random sequences” or “low-discrepancy sequences”. PythonBiogeme implements the Halton draws, from Halton (1960). They have been reported to perform well for discrete choice models (Train, 2000, Bhat, 2001, Bhat, 2003, Sándor and Train, 2004).

The third method to generate uniform random numbers implemented in PythonBiogeme is called “Modified Latin Hypercube Sampling”, and has been proposed by Hess et al. (2006).

In the following, we are using these three options, and compare the accuracy of the corresponding Monte-Carlo integration.

3 Illustration with PythonBiogeme

We first illustrate the method on a simple integral. Consider

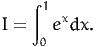(12)

In this case, it can be solved analytically:

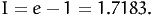(13)

In order to use Monte-Carlo integration, we consider the random variable X that is uniformly distributed on [0,1], so that

(14)

Therefore, we can approximate I by generating R draws from X and

(15)

Moreover, as

(16)

the standard error is 0.0034787613 for R = 20000, and 0.0011000809 for R = 200000. These theoretical values are estimated also below using PythonBiogeme.

We use PythonBiogeme to calculate (15). Note that PythonBiogeme requires a data file, which is not necessary in this simplistic case. We use the simulation mode of PythonBiogeme. It generates output for each row of the data file. In our case, we just need one output, so that we take any data file, and exclude all rows of the file except the first one, using the following syntax:

For this specific example, the data included in the file are irrelevant. The generation of draws in PythonBiogeme is performed using the command bioDraws(’U’), where the argument ’U’ provides the name of the random variable associated with the draws. The distribution of the random variable is specified using the following syntax:

Note that the valid keywords are

• UNIFORM, for a uniform distribution on the interval [0,1],
• UNIFORMSYM, for a uniform distribution on the interval [-1,1],
• NORMAL, for a standard normal distribution, and
• TRUNCNORMAL, for a truncated standard normal distribution. The truncation is defined by the parameter NormalTruncation:
  BIOGEME_OBJECT.PARAMETERS[’NormalTruncation’] = "1.96"

The integrand is defined by the following statement:

and the Monte-Carlo integration is obtained as follows:

The number of draws is defined by the parameter NbrOfDraws:

We calculate as well the simulated variance, using (10):

and the standard error (11):

Also, as we know the true value of the integral

we can calculate the error:

The calculation is obtained using the following statements:

We obtain the following results:

Remember that the true variance is 0.2420356075, and the true standard error is 0.0034787613. If we use ten times more draws, that is 200,000 draws, we obtain a more precise value:

Remember that the true variance is 0.2420356075, and the true standard error is 0.0011000809. The complete specification file for PythonBiogeme is available in Appendix A.1.

4 Variance reduction

There are several techniques to reduce the variance of the draws used for the Monte-Carlo integration. Reducing the variance improves the precision of the approximation for the same number of draws. Equivalently, they allow to use less draws to achieve the same precision. We introduce two of them in this document: antithetic draws, and control variates. As the focus of this document is on PythonBiogeme, we urge the reader to read an introduction to variance reduction methods in simulation, for instance in Ross (2012).

4.1 Antithetic draws

Instead of drawing from X, consider two random variables X₁ and X₂, identically distributed with pdf f_X = f_X1 = f_X2, and define a new random variable

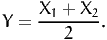(17)

Then, as E[Y] = E[X₁] = E[X₂] = E[X], we can rewrite (1) as follows:

(18)

The variance of this quantity is

(19)

If X₁ and X₂ are independent, this variance is equal to

(20)

Therefore, using Y for Monte-Carlo integration is associated with a variance divided by two, but requires twice more draws (R draws for X₁ and R draws for X₂). It has no advantage on drawing directly R draws from X. Formally, we can compare the standard errors of the two methods for the same number of draws. Drawing 2R draws from X, we obtain the following standard error:

(21)

Drawing R draws from X₁ and R draws from X₂ to generate R draws from Y, we obtain the same standard error

(22)

However, if the variables X₁ and X₂ happen to be negatively correlated, that is if Cov(X₁,X₂) < 0, then Var[Y] < Var[X]∕2, and drawing from Y reduces the standard error. For instance, if X₁ is uniformly distributed on [0,1], then X₂ = 1 - X₁ is also uniformly distributed on [0,1], and

(23)

If X₁ has a standard normal distribution, that is such that E[X₁] = 0 and Var[X₁] = 1, then X₂ = -X₁ has also a standard normal distribution, and is negatively correlated with X₁, as

(24)

The other advantage of this method is that we can recycle the draws. Once we have generated the draws x_r from X₁, the draws from X₂ are obtained using 1 - x_r and -x_r, respectively.

Now, we have to be careful when this technique is used for the general case (2). Indeed, it must be verified first that g(X₁) and g(X₂) are indeed negatively correlated. And it is not guaranteed by the fact that X₁ and X₂ are negatively correlated. Consider two examples.

First, consider g(X) = 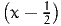². Applying the antithetic method with

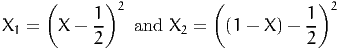(25)

does not work, as

(26)

Actually, applying the antithetic method would increase the variance here, which is not desirable.

Second, consider g(X) = e^X, as in the example presented in Section 3. We apply the antithetic method using

(27)

Here, the two transformed random variables are negatively correlated:

(28)

Therefore, the variance of Y given by (19) is 0.0039124969, as opposed to 0.2420356075∕2 = 0.1210178037 if the two sets of draws were independent. It means that for 10000 draws from Y, the standard error decreases from 0.0034787613 down to 0.0006254996. Moreover, as we use recycled draws, we need only 10000 draws instead of 20000.

To apply this technique in PythonBiogeme, the integrand is defined as follows:

and the number of draws reduced to 10000:

We obtain the following results:

The reader can compare these values with the theoretical derivation presented above. The complete specification file for PythonBiogeme is available in Appendix A.2.

4.2 Control variate

The control variate method reduces the variance by exploiting information from another random variable, correlated with g(X), with a known mean. Consider the random variable Y such that E[Y] = μ. We define a new random variable Z as follows:

(29)

where c ∈ℝ is a parameter. By construction, E[Z] = E[g(X)] for any c, so that draws from Z can be used instead of draws from g(X) for Monte-Carlo integration. Note that we do not need any assumption on g here. The idea is to identify the value of c that minimizes the variance of Z. We have

(30)

which is minimized for

(31)

Therefore, we use for Monte-Carlo integration the random variable

(32)

with variance

(33)

Note that, as for antithetic draws, this technique exploits the correlation between two random variables. If Y is independent from g(X), no variance reduction is achieved.

In our example, g(X) = e^X. If we select Y = X, we know that

(34)

Moreover,

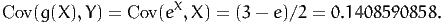(35)

Therefore, we obtain

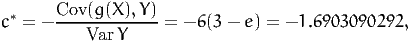(36)

and the variance of Z^* is 0.0039402229, which is much lower than the variance of x, that is 0.2420356075. It means that, for 20000 draws, the standard error is 0.0004438594, as opposed to 0.0034787613. With this method, only 326 draws are sufficient to achieve the same precision as the Monte-Carlo integration without control variate. Indeed,

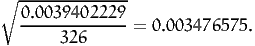(37)

This is a tremendous saving. The control variate method is invoked in PythonBiogeme using the following statement:

where the second argument bioDraws(’U’) is Y, and the third, 0.5, is μ. Note that, in addition to the output requested by the user, PythonBiogeme also generates a report containing statistics on g(X), Y and Z^*. In particular, it reports both the simulated value of Y and μ to detect any implementation error.

The results of the Monte-Carlo integration are:

Simulated Integral (E[Z*])	1.	71759
Simulated Integral (E[X])	1.	72007
Analytical Integral	1.	71828
Sample variance (Var[X])	0.	239849
Std Error ()	0.	000440564
Error	-0.	00069233

The complete specification file for PythonBiogeme is available in Appendix A.3.

Finally, we present in Table 1 the results of the three methods, using different types of uniform draws as described in Section 2. For each technique, the standard errors for the three types of draws are comparable, with the antithetic draws achieving the best value, followed by the control variate. However, the precision actually achieved is much better for Halton, and even more for MLHS.

We encourage the reader to perform similar tests for other simple integrals. For instance,

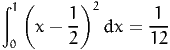(38)

or

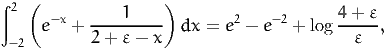(39)

where ε > 0. Note that the domain of integration is not [0,1].

5 Mixtures of logit

Consider an individual n, a choice set 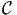_n, and an alternative i ∈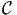_n. The probability to choose i is given by the choice model:

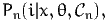(40)

where x is a vector of explanatory variables and θ is a vector of parameters to be estimated from data. In the random utility framework, a utility function is defined for each individual n and each alternative i ∈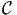_n:

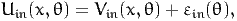(41)

where V_in(x,θ) is deterministic and ε_in is a random variable independent from x. The model is then written:

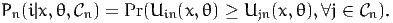(42)

Specific models are obtained from assumptions about the distribution of ε_in. Namely, if ε_in are i.i.d. (across both i and n) extreme value distributed, we obtain the logit model:

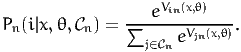(43)

Mixtures of logit are obtained when some of the parameters θ are distributed instead of being fixed. Denote θ = (θ_f,θ_d), where θ_f is the vector of fixed parameters, while θ_d is the vector of distributed parameters, so that the choice model, conditional on θ_d, is

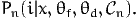(44)

A distribution is to be assumed for θ_d. We denote the pdf of this distribution by f_θd(ξ;γ), where γ contains the parameters of the distribution. Parameters γ are sometimes called the deep parameters of the model. Therefore, the choice model becomes:

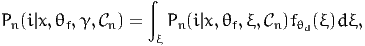(45)

where θ_f and γ must be estimated from data. The above integral has no analytical solution, even when the kernel P_n(i|x,θ_f,ξ,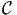_n) is a logit model. Therefore, it must be calculated with numerical integration or Monte-Carlo integration. We do both here to investigate the precision of the variants of Monte-Carlo integration.

5.1 Comparison of integration methods on one integral

We consider the Swissmetro example (Bierlaire et al., 2001). The data file is available from biogeme.epfl.ch. Consider the following specification:

• Variables x: see variables in the data file and new variables defined in Section A.4.
• Fixed parameters θ_f
  ASC_CAR = 0.137 
  ASC_TRAIN = -0.402 
  ASC_SM = 0 
  B_COST = -1.29
• Deep parameters γ:
  B_TIME = -2.26 
  B_TIME_S = 1.66
• We define the coefficient of travel time to be distributed, using the random variable omega, that is assumed to be normally distributed:
  B_TIME_RND = B_TIME + B_TIME_S * omega

  The parameter B_TIME is the mean of B_TIME_RND, and B_TIME_S² is its variance. Note that B_TIME_S is not the standard deviation, and can be positive of negative.

• Utility functions V_in:
  V1 = ASC_TRAIN + \ 
       B_TIME_RND * TRAIN_TT_SCALED + \ 
       B_COST * TRAIN_COST_SCALED 
  V2 = ASC_SM + \ 
       B_TIME_RND * SM_TT_SCALED + \ 
       B_COST * SM_COST_SCALED 
  V3 = ASC_CAR + \ 
       B_TIME_RND * CAR_TT_SCALED + \ 
       B_COST * CAR_CO_SCALED 
  V = {1: V1, 2: V2, 3: V3}
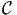• Choice set _n, characterized by the availability conditions:
  CAR_AV_SP = \ 
    DefineVariable(’CAR_AV_SP’,CAR_AV  * (  SP   !=  0  )) 
  TRAIN_AV_SP = \ 
    DefineVariable(’TRAIN_AV_SP’,TRAIN_AV  * (  SP   !=  0  )) 
  av = {1: TRAIN_AV_SP, 
        2: SM_AV, 
        3: CAR_AV_SP}

As there is only one random parameter, the model (45) can be calculated using numerical integration. It is done in PythonBiogeme using the following procedure:

1. Mention that omega is a random variable:
   omega = RandomVariable(’omega’)
2. Define its pdf:
   density = normalpdf(omega).

   Make sure that the library distributions is loaded in order to use the function normalpdf, using the following statement:

   from distributions import *
3. Define the integrand from the logit model, where the probability of the alternative observed to be chosen is calculated (which is typical when calculating a likelihood function):
   integrand = bioLogit(V,av,CHOICE)
4. Calculate the integral:
   analyticalI = Integrate(integrand*density,’omega’)

The complete specification file for PythonBiogeme is available in Appendix A.4. The value of the choice model for first observation in the data file is

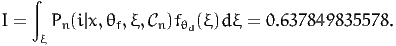(46)

Note that, in order ot obtain so many significant digits, we have used the following statement:

To calculate the same integral with Monte-Carlo integration, we use the same syntax as described earlier in this document:

The complete specification file for PythonBiogeme is available in Appendix A.5. Using the result of the numerical integration as the “true” value of the integral, We obtain the following results:

We now apply the variance reduction methods. The antithetic draws described in Section 4.1 are generated as follows:

1. As we are dealing with draws from the normal distribution, the antithetic draw of x_r is -x_r. We create two versions of the parameter, one with the draw, and one with its antithetic:
   B_TIME_RND = B_TIME + B_TIME_S * bioDraws(’B_TIME_RND’) 
   B_TIME_RND_MINUS = B_TIME - B_TIME_S * bioDraws(’B_TIME_RND’)
2. Consistently, we then generate two versions of the model:
   V1_MINUS = ASC_TRAIN + \ 
              B_TIME_RND_MINUS * TRAIN_TT_SCALED + \ 
              B_COST * TRAIN_COST_SCALED 
   V2_MINUS = ASC_SM + \ 
              B_TIME_RND_MINUS * SM_TT_SCALED + \ 
              B_COST * SM_COST_SCALED 
   V3_MINUS = ASC_CAR + \ 
              B_TIME_RND_MINUS * CAR_TT_SCALED + \ 
              B_COST * CAR_CO_SCALED 
   V_MINUS = {1: V1_MINUS, 
              2: V2_MINUS, 
              3: V3_MINUS}
3. The integrand is the average of the integrands generated by the two versions of the model:
   integrand_plus = bioLogit(V,av,CHOICE) 
   integrand_minus = bioLogit(V_MINUS,av,CHOICE) 
   integrand = 0.5 * (integrand_plus + integrand_minus)

The complete specification file for PythonBiogeme is available in Appendix A.6.

The control variate method, described in Section 4.2, requires an output of the simulation such that the analytical integral is known. We propose here to consider

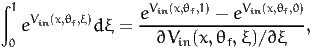(47)

if ∂V_in(x,θ_f,ξ)∕∂ξ does not depend on ξ. This integral is calculated by Monte-Carlo after recycling the uniform draws used to generate the normal draws for the original integration. We follow the following procedure:

1. We recycle the draws:
   UNIFDRAW = bioRecycleDraws(’B_TIME_RND’)
2. We calculate the control variate integrand:
   VCV = ASC_TRAIN + \ 
         (B_TIME + B_TIME_S * UNIFDRAW) * TRAIN_TT_SCALED + \ 
         B_COST * TRAIN_COST_SCALED

   Note that the derivative with respect to UNIFDRAW is

   B_TIME_S * TRAIN_TT_SCALED$.
3. We provide the analytical value of the control variate integral:
   VCV_ZERO = ASC_TRAIN + \ 
              B_TIME * TRAIN_TT_SCALED + \ 
              B_COST * TRAIN_COST_SCALED 
   VCV_ONE = ASC_TRAIN + \ 
            (B_TIME + B_TIME_S ) * TRAIN_TT_SCALED + \ 
            B_COST * TRAIN_COST_SCALED 
   VCV_INTEGRAL = (exp(VCV_ONE) - exp(VCV_ZERO)) / \ 
                  (B_TIME_S * TRAIN_TT_SCALED)
4. We perform the Monte-Carlo integration:
   simulatedI = MonteCarloControlVariate(integrand,\ 
                                         exp(VCV),\ 
                                         VCV_INTEGRAL)

The complete specification file for PythonBiogeme is available in Appendix A.7.

Table 2 provides the results of the Monte-Carlo integration using different variance reduction methods (none, antithetic and control variates), different uniform draws (pseudo, Halton and MLHS), and different number of draws.

We can observe the following:

• In terms of standard errors of the draws, the Monte-Carlo integration without variance reduction has a standard error about 7.5 times as large as the anthitetic version, and 2 times as large as the control variate.
• In terms of absolute error, when compared to the value provided by the numerical integration, the error of the Monte-Carlo integration without variance reduction is about the same for the pseudo draws, 12 times larger for the Halton draws, and 25 times larger for the MHLS draws, when compared to the antithetic draws. If it between 3 and 4 times larger, when compared to the control variates.
• There is no significant difference in terms of standard errors across the types of draws, irrespectively of the variance reduction method used.
• In terms of actual error, though, the Halton draws improves the precision of the output, and the MHLS even more.
• Using the antithetic draws with 1000 draws achieves a similar precision as no variance reduction with 20000 draws.
• Using the control variates with 2000 draws achieves a similar precision as no variance reduction with 20000 draws.
• Reducing the number of draws to 500 does not deteriorate much the precision for the antithetic draws.

It would be useful to perform the same experiment for some other observations in the data file. Such experiments can give useful insights to for the choice of the most appropriate integration technique. In the following, we compare some of these techniques for the maximum likelihood estimation of the parameters of the model.

5.2 Comparison of integration methods for maximum likelihood estimation

We now estimate the parameters of the model using all observations in the data set associated with work trips. Observations such that the dependent variable CHOICE is 0 are also removed.

The estimation using numerical integration is performed using the following statements:

The complete specification file for PythonBiogeme is available in Appendix A.8.

For Monte-Carlo integration, we use the following statements:

where the statement l = mixedloglikelihood(prob) is equivalent to

The complete specification file for PythonBiogeme is available in Appendix A.9.

The following estimation results are presented:

• Table 4: numerical integration;
• Table 5: Monte-Carlo integration, no variance reduction, 2000 MHLS draws;
• Table 6: antithetic draws, 1000 MHLS draws;
• Table 7: control variates, 2000 MHLS draws;
• Table 8: Monte-Carlo integration, 500 MHLS draws;
• Table 9: antithetic draws, 250 MHLS draws;
• Table 10: control variates, 500 MHLS draws.

The final log likelihood in each case, as well as the estimation time are summarized in Table 3. In this experiment, when looking at the estimates, it seems that the MLHS draws provide relatively good precision, even for a lower number of draws, and with no variance reduction. Clearly, this result cannot be generalized, and should be investigated on a case by case basis. Note however that the default type of draws in PythonBiogeme is MLHS, because it is performing particularly well in this example.

---

Robust Parameter Coeff. Asympt. number Description estimate std. error t-stat p-value 1 ASC_CAR 0. 137 0. 0517 2. 65 0. 01 2 ASC_TRAIN -0. 401 0. 0656 -6. 12 0. 00 3 B_COST -1. 29 0. 0863 -14. 90 0. 00 4 B_TIME -2. 26 0. 117 -19. 38 0. 00 5 B_TIME_S -1. 65 0. 125 -13. 26 0. 00

Summary statistics Number of observations = 6768 Number of excluded observations = 3960 Number of estimated parameters = 5 Number of iterations = 13 Estimation time: 00 : 02 : 37 (β0) = -7157.671 () = -5214.879 -2[(β0) - ()] = 3885.585 ρ2 = 0.271 ρ2 = 0.271

Table 4: Estimation results with numerical integration

---

---

Robust Parameter Coeff. Asympt. number Description estimate std. error t-stat p-value 1 ASC_CAR 0. 137 0. 0517 2. 65 0. 01 2 ASC_TRAIN -0. 402 0. 0658 -6. 10 0. 00 3 B_COST -1. 29 0. 0864 -14. 89 0. 00 4 B_TIME -2. 26 0. 117 -19. 31 0. 00 5 B_TIME_S 1. 66 0. 132 12. 59 0. 00

Summary statistics Number of observations = 6768 Number of excluded observations = 3960 Number of estimated parameters = 5 Number of iterations = 9 Estimation time: 00 : 31 : 11 (β0) = -6964.663 () = -5214.835 -2[(β0) - ()] = 3499.656 ρ2 = 0.251 ρ2 = 0.251

Table 5: Estimation results with Monte-Carlo, no variance reduction, 2000 MHLS draws

---

---

Robust Parameter Coeff. Asympt. number Description estimate std. error t-stat p-value 1 ASC_CAR 0. 137 0. 0517 2. 65 0. 01 2 ASC_TRAIN -0. 402 0. 0658 -6. 10 0. 00 3 B_COST -1. 29 0. 0863 -14. 89 0. 00 4 B_TIME -2. 26 0. 117 -19. 31 0. 00 5 B_TIME_S 1. 66 0. 132 12. 59 0. 00

Summary statistics Number of observations = 6768 Number of excluded observations = 3960 Number of estimated parameters = 5 Number of iterations = 12 Estimation time: 00 : 39 : 26 (β0) = -7155.875 () = -5214.899 -2[(β0) - ()] = 3881.952 ρ2 = 0.271 ρ2 = 0.271

Table 6: Estimation results with antithetic draws, 1000 MHLS draws

---

---

Robust Parameter Coeff. Asympt. number Description estimate std. error t-stat p-value 1 ASC_CAR 0. 137 0. 0517 2. 65 0. 01 2 ASC_TRAIN -0. 402 0. 0658 -6. 10 0. 00 3 B_COST -1. 29 0. 0864 -14. 89 0. 00 4 B_TIME -2. 26 0. 117 -19. 31 0. 00 5 B_TIME_S 1. 66 0. 132 12. 59 0. 00

Summary statistics Number of observations = 6768 Number of excluded observations = 3960 Number of estimated parameters = 5 Number of iterations = 12 Estimation time: 00 : 42 : 11 (β0) = -7155.867 () = -5214.835 -2[(β0) - ()] = 3882.063 ρ2 = 0.271 ρ2 = 0.271

Table 7: Estimation results with control variates, 2000 MHLS draws

---

---

Robust Parameter Coeff. Asympt. number Description estimate std. error t-stat p-value 1 ASC_CAR 0. 137 0. 0517 2. 65 0. 01 2 ASC_TRAIN -0. 402 0. 0658 -6. 10 0. 00 3 B_COST -1. 29 0. 0864 -14. 88 0. 00 4 B_TIME -2. 26 0. 117 -19. 33 0. 00 5 B_TIME_S 1. 66 0. 131 12. 63 0. 00

Summary statistics Number of observations = 6768 Number of excluded observations = 3960 Number of estimated parameters = 5 Number of iterations = 12 Estimation time: 00 : 09 : 26 (β0) = -7155.962 () = -5214.940 -2[(β0) - ()] = 3882.044 ρ2 = 0.271 ρ2 = 0.271

Table 8: Estimation results with Monte-Carlo integration, no variance reduction, 500 MHLS draws

---

---

Robust Parameter Coeff. Asympt. number Description estimate std. error t-stat p-value 1 ASC_CAR 0. 137 0. 0517 2. 65 0. 01 2 ASC_TRAIN -0. 402 0. 0658 -6. 11 0. 00 3 B_COST -1. 29 0. 0864 -14. 88 0. 00 4 B_TIME -2. 26 0. 117 -19. 33 0. 00 5 B_TIME_S 1. 66 0. 131 12. 61 0. 00

Summary statistics Number of observations = 6768 Number of excluded observations = 3960 Number of estimated parameters = 5 Number of iterations = 12 Estimation time: 00 : 09 : 21 (β0) = -7155.877 () = -5214.897 -2[(β0) - ()] = 3881.960 ρ2 = 0.271 ρ2 = 0.271

Table 9: Estimation results with antithetic draws, 250 MHLS draws

---

---

Robust Parameter Coeff. Asympt. number Description estimate std. error t-stat p-value 1 ASC_CAR 0. 137 0. 0517 2. 65 0. 01 2 ASC_TRAIN -0. 402 0. 0658 -6. 10 0. 00 3 B_COST -1. 29 0. 0864 -14. 88 0. 00 4 B_TIME -2. 26 0. 117 -19. 33 0. 00 5 B_TIME_S 1. 66 0. 131 12. 63 0. 00

Summary statistics Number of observations = 6768 Number of excluded observations = 3960 Number of estimated parameters = 5 Number of iterations = 12 Estimation time: 00 : 08 : 59 (β0) = -7155.962 () = -5214.940 -2[(β0) - ()] = 3882.044 ρ2 = 0.271 ρ2 = 0.271

Table 10: Estimation results with control variates, 500 MHLS draws

---

6 Conclusion

This document describes the variants of Monte-Carlo integration, and suggests how to perform some analysis using the SIMULATE operator of PythonBiogeme, that helps investigating the performance of each of them before starting a maximum likelihod estimation, that may take a while to converge. In the example provided in this document, the antithetic draws method, combined with MLHS appeared to be the most precise. This result is not universal. The analysis must be performed on a case by case basis.

A Complete specification files

A.1 01simpleIntegral.py

A.2 02antithetic.py

A.3 03controlVariate.py

A.4 05normalMixtureTrueAnalytical.py