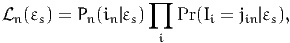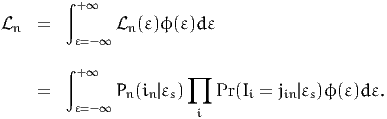Estimating choice models with latent variables
with PythonBiogeme
Michel Bierlaire
June 28, 2016
Report TRANSP-OR 160628
Transport and Mobility Laboratory
School of Architecture, Civil and Environmental Engineering
Ecole Polytechnique Fédérale de Lausanne
transp-or.epfl.ch
The package PythonBiogeme (biogeme.epfl.ch) is designed to estimate
the parameters of various models using maximum likelihood estimation.
It is particularly designed for discrete choice models. In this document,
we present how to estimate choice models involving latent variables. We
assume that the reader is already familiar with discrete choice models,
with latent variables, and with PythonBiogeme. This document has been
written using PythonBiogeme 2.5, but should remain valid for future
versions.
1 Models and notations
The literature on discrete choice models with latent variables is vast (Walker, 2001,
Ashok et al., 2002, Greene and Hensher, 2003, Ben-Akiva et al., 2002, to cite
just a few). We start this document by a short introduction to the models and the
notations.
A latent variable is a variable that cannot be directly observed. Therefore, it is
a random variable, usually characterized by a structural equation:
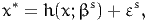 | (1) |
where x is a vector of explanatory variables (observed or latent), βs is a vector
of Ks parameters (to be estimated from data) and εs is the (random)
error term. Note that the most common specification for the function h is
linear:
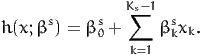 | (2) |
In discrete choice, the utility Uin that an individual n associates with an
alternative i is a latent variable.
The analyst obtains information about latent variables from indirect
measurements. They are manifestations of the underlying latent entity. For
example, in discrete choice, utility is not observed, but is estimated from the
observation of actual choices. The relationship between a latent variable and
measurements is characterized by measurement equations.
The first type of measurement equation is designed to capture potential biases
occurring when the latent variable is reported. The measurement equation has the
following form:
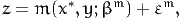 | (3) |
where z is the reported value, x* is the latent variable, y is a vector of observed
explanatory variables, βm is a vector of Km parameters (to be estimated from
data) and εm is the (random) error term. Note that the most common
specification for the function m is linear:
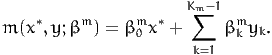 | (4) |
Another measurement equation is necessary when discrete ordered variables
are available. It is typical in our context. First, the choice, as indicator
of the utility of an alternative, is a binary variable (the alternative is
chosen or not). Second, psychometric indicators revealing latent variables
associated with attitudes and perceptions are most of the time coded
using a Likert scale (Likert, 1932). Suppose that the measurement is
represented by an ordered discrete variable I taking the values j1, j2, …, jM, we
have
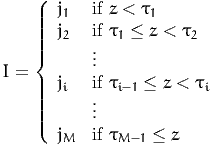 | (5) |
where z is defined by (3), and τ1, …. τM-1 are parameters to be estimated, such
that
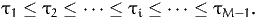 | (6) |
The probability of a given response ji is
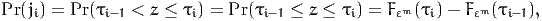 | (7) |
where Fεm is the cumulative distribution function (CDF) of the error term εm.
When a normal distribution is assumed, the model (7) is called ordered
probit.
Note that the Likert scale, as proposed by Likert (1932), has M = 5
levels:
- strongly approve,
- approve,
- undecided,
- disapprove,
- strongly disapprove.
In the choice context, there are two categories: chosen, or not chosen, so that
M = 2. Considering alternative i for individual n, the variable zin is the
difference
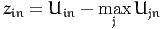 | (8) |
between the utility of alternative i and the largest utility among all alternatives,
so that
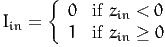 | (9) |
which is (5) with M = 2 and τ1 = 0.
2 Indirect measurement of latent variables
The indirect measurement of latent variables is usually done by collecting various
indicators. A list of statements is provided to the respondent, and she is asked to
react to each of them using a Likert scale, as defined above. Although these
statements have been designed to capture some pre-determined aspects, it is
useful to identify what are the indicators that reveal most of the information
about the latent variables.
We consider an example based on data collected in Switzerland in 2009
and 2010 (Atasoy et al., 2011, Atasoy et al., 2013). Various indicators,
revealing various attitudes about the environment, about mobility, about
residential preferences, and about lifestyle, have been collected, as described in
Table 12.
We first perform an exploratory factor analysis on the indicators. For
instance, the code in Section B.1 performs this task using the package R
(www.r-project.org).
The results are
Factor1 Factor2 Factor3 Envir01 -0.565 Envir02 -0.407 Envir03 0.414 Mobil11 0.484 Mobil14 0.473 Mobil16 0.462 Mobil17 0.434 Mobil26 0.408 ResidCh01 0.577 ResidCh04 0.406 ResidCh05 0.635 ResidCh06 0.451 ResidCh07 -0.418 LifSty07 0.430
The first factor is explained by the following indicators:
-
Envir01
- Fuel price should be increased to reduce congestion and air
pollution.
-
Envir02
- More public transportation is needed, even if taxes are set to pay
the additional costs.
-
Envir03
- Ecology disadvantages minorities and small businesses.
-
Mobil11
- It is difficult to take the public transport when I carry bags or
luggage.
-
Mobil14
- When I take the car I know I will be on time.
-
Mobil16
- I do not like changing the mean of transport when I am traveling.
-
Mobil17
- If I use public transportation I have to cancel certain activities I
would have done if I had taken the car.
We decide to label the associated latent variable “car lover”. Note
the sign of the loading factors, and the associated interpretation of the
statements.
In order to write the structural equation (1), we first define some variables
from the data file.
- age_65_more: the respondent is 65 or older;
- moreThanOneCar: the number of cars in the household is strictly greater
than 1;
- moreThanOneBike: the number of bikes in the household is strictly greater
than 1;
- individualHouse: the type of house is individual or terraced;
- male: the respondent is a male;
- haveChildren: the family is a couple or a single with children;
- haveGA: the respondent owns a season ticket;
- highEducation: the respondent has obtained a degree strictly higher than
high school.
We also want to include income. As it is a continuous variable, and strict
linearity is not appropriate, we adopt a piecewise linear (or spline) specification.
To do so, we define the following variables:
- ScaledIncome: income, in 1000 CHF;
- ContIncome_0_4000: min(ScaledIncome,4)
- ContIncome_4000_6000: max(0,min(ScaledIncome-4,2))
- ContIncome_6000_8000: max(0,min(ScaledIncome-6,2))
- ContIncome_8000_10000: max(0,min(ScaledIncome-8,2))
- ContIncome_10000_more: max(0,ScaledIncome-10)
The structural equation is therefore
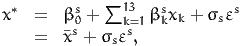 | (10) |
where εs is a random variable normally distributed with mean 0 and variance
1:
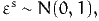 | (11) |
and
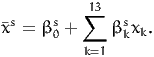 | (12) |
2.1 Indicators as continuous variables
Consider now the measurement equations (3), assuming that the indicators
provided by the respondents are continuous, that is that the indicators Ii are used
for z in (3). Although this is not formally correct, we assume it first to
present corresponding the formulation. We are describing the correct way in
Section 2.2.
We define the measurement equation for indicator i as
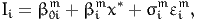 | (13) |
where
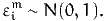 | (14) |
Using (10) into (13), we obtain
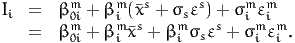 | (15) |
The quantity
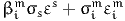 | (16) |
is normally distributed as
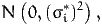 | (17) |
where (σi*)2 = (βimσs)2 + (σim)2. The parameter σs is normalized to 1, so
that
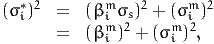
and
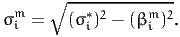
Therefore, we rewrite the measurement equations as
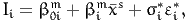 | (18) |
where εi* ~ N(0,1). Not all these parameters can be estimated from data. We
need to set the units of the latent variable. It is decided to set it to the first
indicator (i = 1), by normalizing β01 = 0 and β1m = -1. Note the -1 coefficient,
capturing the fact that the first indicator increases when the car loving attitude
decreases, as revealed by the factor analysis results, and confirmed by the
interpretation.
The implementation of this model in PythonBiogeme is reported in
Section B.2.
The statement
loglikelihoodregression(Envir01,MODEL_Envir01,SIGMA_STAR_Envir01)
provides the log likelihood for the linear regression, where Envir01 is the
dependent variable Ii, MODEL_Envir01 is the model β0im + βimxs, CARLOVERS is
xs and SIGMA_STAR_Envir01 is the scale parameter σi*. Note that there are
missing data. If the dependent variable is not positive or equal to 6, the value
should be ignored and the log likelihood set to 0. This is implemented using the
following statement:
Elem({0:0, \ 1:loglikelihoodregression(Envir01,MODEL_Envir01,SIGMA_STAR_Envir01)},\ (Envir01 > 0)*(Envir01 < 6))
The dictionary F gathers, for each respondent, the log likelihood of the 7
indicators. The statement
calculates the total log likelihood for a given respondent of all 7 indicators
together.
The estimation results are reported in Tables 1 and 2, where for each
indicator i,
- INTER_i is the intercept β0im,
- B_i is the coefficient βim,
- SIGMA_STAR_i is the scale σi*,
in (18).
Table 1: Estimation results for the linear regression
| | | | Robust | | | Parameter | | Coeff. | Asympt. | |
| number | Description | estimate | std. error | t-stat | p-value
|
|
|
|
|
|
|
|
|
|
| | 1 | INTER_Envir02 | 2. | 01 | 0. | 153 | 13. | 10 | 0. | 00 | | 2 |
INTER_Envir03 | 4. | 57 | 0. | 158 | 28. | 85 | 0. | 00 | | 3 |
INTER_Mobil11 | 5. | 14 | 0. | 151 | 34. | 04 | 0. | 00 | | 4 |
INTER_Mobil14 | 4. | 91 | 0. | 157 | 31. | 21 | 0. | 00 | | 5 |
INTER_Mobil16 | 4. | 80 | 0. | 158 | 30. | 28 | 0. | 00 | | 6 |
INTER_Mobil17 | 4. | 50 | 0. | 157 | 28. | 64 | 0. | 00 | | 7 |
L_Envir02_F1 | -0. | 496 | 0. | 0578 | -8. | 59 | 0. | 00 | | 8 |
L_Envir03_F1 | 0. | 671 | 0. | 0601 | 11. | 16 | 0. | 00 | | 9 |
L_Mobil11_F1 | 0. | 563 | 0. | 0589 | 9. | 56 | 0. | 00 | | 10 |
L_Mobil14_F1 | 0. | 705 | 0. | 0596 | 11. | 83 | 0. | 00 | | 11 |
L_Mobil16_F1 | 0. | 540 | 0. | 0612 | 8. | 82 | 0. | 00 | | 12 |
L_Mobil17_F1 | 0. | 432 | 0. | 0600 | 7. | 20 | 0. | 00 | | 13 |
SIGMA_STAR_Envir01 | 1. | 25 | 0. | 0161 | 77. | 34 | 0. | 00 | | 14 |
SIGMA_STAR_Envir02 | 1. | 12 | 0. | 0149 | 75. | 04 | 0. | 00 | | 15 |
SIGMA_STAR_Envir03 | 1. | 07 | 0. | 0155 | 68. | 92 | 0. | 00 | | 16 |
SIGMA_STAR_Mobil11 | 1. | 08 | 0. | 0163 | 66. | 40 | 0. | 00 | | 17 |
SIGMA_STAR_Mobil14 | 1. | 05 | 0. | 0141 | 74. | 62 | 0. | 00 | | 18 |
SIGMA_STAR_Mobil16 | 1. | 10 | 0. | 0151 | 72. | 55 | 0. | 00 | | 19 |
SIGMA_STAR_Mobil17 | 1. | 11 | 0. | 0155 | 71. | 74 | 0. | 00 | | |
|
Table 2: Estimation results for the linear regression (ctd)
| | | | Robust | | | Parameter | | Coeff. | Asympt. | |
| number | Description | estimate | std. error | t-stat | p-value
|
|
|
|
|
|
|
|
|
|
| | 20 | coef_ContIncome_0_4000 | 0. | 103 | 0. | 0633 | 1. | 63 | 0. | 10 | | 21 |
coef_ContIncome_10000_more | 0. | 103 | 0. | 0360 | 2. | 86 | 0. | 00 | | 22 |
coef_ContIncome_4000_6000 | -0. | 252 | 0. | 108 | -2. | 33 | 0. | 02 | | 23 |
coef_ContIncome_6000_8000 | 0. | 300 | 0. | 130 | 2. | 31 | 0. | 02 | | 24 |
coef_ContIncome_8000_10000 | -0. | 621 | 0. | 150 | -4. | 13 | 0. | 00 | | 25 |
coef_age_65_more | 0. | 103 | 0. | 0732 | 1. | 41 | 0. | 16 |
| 26 | coef_haveChildren | -0. | 0454 | 0. | 0542 | -0. | 84 | 0. | 40 | | 27 |
coef_haveGA | -0. | 689 | 0. | 0861 | -8. | 00 | 0. | 00 | | 28 |
coef_highEducation | -0. | 298 | 0. | 0612 | -4. | 87 | 0. | 00 |
| 29 | coef_individualHouse | -0. | 110 | 0. | 0540 | -2. | 04 | 0. | 04 | | 30 |
coef_intercept | -2. | 50 | 0. | 183 | -13. | 66 | 0. | 00 |
| 31 | coef_male | 0. | 0716 | 0. | 0506 | 1. | 41 | 0. | 16 | | 32 |
coef_moreThanOneBike | -0. | 328 | 0. | 0621 | -5. | 28 | 0. | 00 | | 33 |
coef_moreThanOneCar | 0. | 624 | 0. | 0581 | 10. | 74 | 0. | 00 |
|
|
|
|
|
|
|
|
|
| | |
|
Summary statistics
| Number of observations = 1906 | Number of excluded observations = 359
| Number of estimated parameters = 33
| 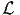 ( (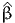 ) ) | = | -20658.648 |
| |
|
2.2 Indicators as discrete variables
We now consider the measurement equations (5). As the measurements are using
a Likert scale with M = 5 levels, we define 4 parameters τi. In order to account
for the symmetry of the indicators, we actually define two positive parameters δ1
and δ2, and define
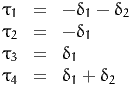
Therefore, the probability of a given response is given by the ordered probit
model:
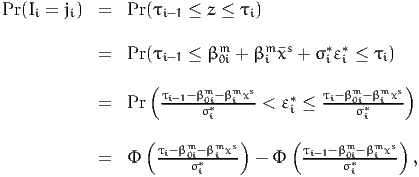 | (19) |
where Φ(⋅) is the CDF of the standardized normal distribution, as illustrated in
Figure 1.
The model specification for PythonBiogeme is reported in Section B.3.
Equation 19 is coded using the following statements:
Envir01_tau_1 = (tau_1-MODEL_Envir01) / SIGMA_STAR_Envir01 Envir01_tau_2 = (tau_2-MODEL_Envir01) / SIGMA_STAR_Envir01 Envir01_tau_3 = (tau_3-MODEL_Envir01) / SIGMA_STAR_Envir01 Envir01_tau_4 = (tau_4-MODEL_Envir01) / SIGMA_STAR_Envir01 IndEnvir01 = { 1: bioNormalCdf(Envir01_tau_1), 2: bioNormalCdf(Envir01_tau_2)-bioNormalCdf(Envir01_tau_1), 3: bioNormalCdf(Envir01_tau_3)-bioNormalCdf(Envir01_tau_2), 4: bioNormalCdf(Envir01_tau_4)-bioNormalCdf(Envir01_tau_3), 5: 1-bioNormalCdf(Envir01_tau_4), 6: 1.0, -1: 1.0, -2: 1.0 } P_Envir01 = Elem(IndEnvir01, Envir01)
Note that the indicators in the data file can take the values -2, -1, 1, 2, 3, 4, 5,
and 6. However, the values 6, -1 and 2 are ignored, and associated with a
probability of 1, so that they have no influence on the total likelihood
function.
Table 3: Estimation results for the ordered probit regression
| | | | Robust | | | Parameter | | Coeff. | Asympt. | |
| number | Description | estimate | std. error | t-stat | p-value
|
|
|
|
|
|
|
|
|
|
| | 1 | B_Envir02_F1 | -0. | 431 | 0. | 0523 | -8. | 25 | 0. | 00 | | 2 |
B_Envir03_F1 | 0. | 566 | 0. | 0531 | 10. | 66 | 0. | 00 | | 3 |
B_Mobil11_F1 | 0. | 484 | 0. | 0533 | 9. | 09 | 0. | 00 | | 4 |
B_Mobil14_F1 | 0. | 582 | 0. | 0514 | 11. | 34 | 0. | 00 | | 5 |
B_Mobil16_F1 | 0. | 463 | 0. | 0543 | 8. | 53 | 0. | 00 | | 6 |
B_Mobil17_F1 | 0. | 368 | 0. | 0519 | 7. | 10 | 0. | 00 | | 7 |
INTER_Envir02 | 0. | 349 | 0. | 0261 | 13. | 35 | 0. | 00 | | 8 |
INTER_Envir03 | -0. | 309 | 0. | 0270 | -11. | 42 | 0. | 00 | | 9 |
INTER_Mobil11 | 0. | 338 | 0. | 0290 | 11. | 66 | 0. | 00 | | 10 |
INTER_Mobil14 | -0. | 131 | 0. | 0251 | -5. | 21 | 0. | 00 | | 11 |
INTER_Mobil16 | 0. | 128 | 0. | 0276 | 4. | 65 | 0. | 00 | | 12 |
INTER_Mobil17 | 0. | 146 | 0. | 0260 | 5. | 60 | 0. | 00 | | 13 |
SIGMA_STAR_Envir02 | 0. | 767 | 0. | 0222 | 34. | 62 | 0. | 00 | | 14 |
SIGMA_STAR_Envir03 | 0. | 718 | 0. | 0206 | 34. | 89 | 0. | 00 | | 15 |
SIGMA_STAR_Mobil11 | 0. | 783 | 0. | 0240 | 32. | 63 | 0. | 00 | | 16 |
SIGMA_STAR_Mobil14 | 0. | 688 | 0. | 0209 | 32. | 98 | 0. | 00 | | 17 |
SIGMA_STAR_Mobil16 | 0. | 754 | 0. | 0226 | 33. | 42 | 0. | 00 | | 18 |
SIGMA_STAR_Mobil17 | 0. | 760 | 0. | 0235 | 32. | 32 | 0. | 00 | | |
|
Table 4: Estimation results for the ordered probit regression (ctd)
| | | | Robust | | | Parameter | | Coeff. | Asympt. | |
| number | Description | estimate | std. error | t-stat | p-value
|
|
|
|
|
|
|
|
|
|
| | 19 | coef_ContIncome_0_4000 | 0. | 0903 | 0. | 0528 | 1. | 71 | 0. | 09 | | 20 |
coef_ContIncome_10000_more | 0. | 0844 | 0. | 0303 | 2. | 79 | 0. | 01 | | 21 |
coef_ContIncome_4000_6000 | -0. | 221 | 0. | 0918 | -2. | 41 | 0. | 02 | | 22 |
coef_ContIncome_6000_8000 | 0. | 259 | 0. | 109 | 2. | 37 | 0. | 02 | | 23 |
coef_ContIncome_8000_10000 | -0. | 523 | 0. | 128 | -4. | 10 | 0. | 00 | | 24 |
coef_age_65_more | 0. | 0717 | 0. | 0613 | 1. | 17 | 0. | 24 |
| 25 | coef_haveChildren | -0. | 0376 | 0. | 0459 | -0. | 82 | 0. | 41 | | 26 |
coef_haveGA | -0. | 578 | 0. | 0750 | -7. | 70 | 0. | 00 | | 27 |
coef_highEducation | -0. | 247 | 0. | 0521 | -4. | 73 | 0. | 00 |
| 28 | coef_individualHouse | -0. | 0886 | 0. | 0455 | -1. | 94 | 0. | 05 | | 29 |
coef_intercept | 0. | 398 | 0. | 153 | 2. | 61 | 0. | 01 |
| 30 | coef_male | 0. | 0664 | 0. | 0433 | 1. | 53 | 0. | 13 | | 31 |
coef_moreThanOneBike | -0. | 277 | 0. | 0538 | -5. | 15 | 0. | 00 | | 32 |
coef_moreThanOneCar | 0. | 533 | 0. | 0516 | 10. | 34 | 0. | 00 | | 33 |
delta_1 | 0. | 252 | 0. | 00726 | 34. | 70 | 0. | 00 | | 34 |
delta_2 | 0. | 759 | 0. | 0193 | 39. | 30 | 0. | 00 |
|
|
|
|
|
|
|
|
|
| | |
|
Summary statistics
| Number of observations = 1906 | Number of excluded observations = 359
| Number of estimated parameters = 34
| 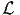 ( (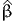 ) ) | = | -17794.883 |
| |
|
3 Choice model
Latent variables can be included in choice models. Consider a model with three
alternatives “public transportation” (PT), “car” (CAR) and “slow modes” (SM).
The utility functions are of the following form:
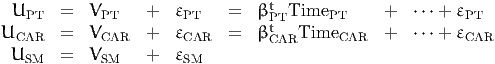 | (20) |
The full specification can be found in the specification file in Section B.4. The
latent variable that we have considered in the previous sections captures the “car
loving” attitude of the individuals. In order to include it in the choice model, we
specify that the coefficients of travel time for the public transportation
alternative, and for the car alternative, vary with the latent variable. We
have
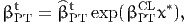 | (21) |
and
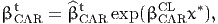 | (22) |
where x* is defined by (10), so that
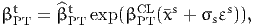 | (23) |
and
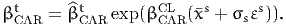 | (24) |
Technically, such a choice model can be estimated using the choice
observations only, without the indicators. Assuming that εPT, εCAR and εSM
are i.i.d. extreme value distributed, we have
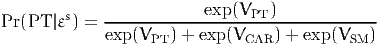 | (25) |
and
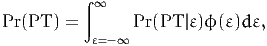 | (26) |
where ϕ(⋅) is the probability density function of the univariate standardized
normal distribution. The choice model is a mixture of logit models. The
estimation results are reported in Table 5, where
- BETA_TIME_PT_CL refers to βCLPT in (21),
- BETA_TIME_PT_REF refers to
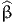 tPT in (21),
tPT in (21),
- BETA_TIME_CAR_CL refers to βCLCAR in (22), and
- BETA_TIME_CAR_REF refers to
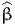 tCAR in (22).
tCAR in (22).
Table 5: Estimation results for the mixture of logit models
| | | | Robust | | | Parameter | | Coeff. | Asympt. | |
| number | Description | estimate | std. error | t-stat | p-value
|
|
|
|
|
|
|
|
|
|
| | 1 | ASC_CAR | 0. | 373 | 0. | 138 | 2. | 70 | 0. | 01 | | 2 |
ASC_SM | 0. | 964 | 0. | 263 | 3. | 66 | 0. | 00 | | 3 |
BETA_COST_HWH | -1. | 77 | 0. | 473 | -3. | 75 | 0. | 00 | | 4 |
BETA_COST_OTHER | -1. | 51 | 0. | 309 | -4. | 89 | 0. | 00 | | 5 |
BETA_DIST | -4. | 88 | 0. | 655 | -7. | 46 | 0. | 00 | | 6 |
BETA_TIME_CAR_CL | -0. | 491 | 0. | 0509 | -9. | 65 | 0. | 00 | | 7 |
BETA_TIME_CAR_REF | -27. | 1 | 6. | 17 | -4. | 39 | 0. | 00 | | 8 |
BETA_TIME_PT_CL | -1. | 75 | 0. | 0906 | -19. | 32 | 0. | 00 | | 9 |
BETA_TIME_PT_REF | -5. | 35 | 2. | 85 | -1. | 88 | 0. | 06 | | 10 |
BETA_WAITING_TIME | -0. | 0517 | 0. | 0175 | -2. | 96 | 0. | 00 | | 11 |
coef_ContIncome_0_4000 | -0. | 102 | 0. | 0907 | -1. | 12 | 0. | 26 | | 12 |
coef_ContIncome_10000_more | -0. | 101 | 0. | 0354 | -2. | 86 | 0. | 00 | | 13 |
coef_ContIncome_4000_6000 | 0. | 0272 | 0. | 121 | 0. | 22 | 0. | 82 | | 14 |
coef_ContIncome_6000_8000 | -0. | 125 | 0. | 214 | -0. | 59 | 0. | 56 | | 15 |
coef_ContIncome_8000_10000 | 0. | 326 | 0. | 188 | 1. | 73 | 0. | 08 | | 16 |
coef_age_65_more | 0. | 199 | 0. | 0858 | 2. | 32 | 0. | 02 |
| 17 | coef_haveChildren | -0. | 0414 | 0. | 0673 | -0. | 61 | 0. | 54 | | 18 |
coef_haveGA | 1. | 33 | 0. | 0869 | 15. | 30 | 0. | 00 | | 19 |
coef_highEducation | -0. | 462 | 0. | 0540 | -8. | 56 | 0. | 00 |
| 20 | coef_individualHouse | 0. | 115 | 0. | 124 | 0. | 92 | 0. | 36 | | 21 |
coef_male | -0. | 133 | 0. | 0567 | -2. | 35 | 0. | 02 | | 22 |
coef_moreThanOneBike | 0. | 152 | 0. | 0977 | 1. | 55 | 0. | 12 | | 23 |
coef_moreThanOneCar | -0. | 598 | 0. | 0669 | -8. | 94 | 0. | 00 |
|
|
|
|
|
|
|
|
|
| | |
|
Summary statistics
| Number of observations = 1906 | Number of excluded observations = 359
| Number of estimated parameters = 23
| 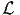 (β0) (β0) | = | -2093.955 |
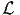 ( (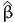 ) ) | = | -1078.003 |
-2[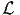 (β0) - (β0) - 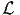 ( (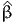 )] )] | = | 2031.905 |
| ρ2 | = | 0.485 |
| ρ2 | = | 0.474 |
| |
|
4 Sequential estimation
In order to exploit both the choice data and the psychometric indicator, we now
combine the latent variable model with the choice model. The easiest way to
estimate a joint model is using sequential estimation. However, such an estimator
is not efficient, and a full information estimation is preferable. It is described in
Section 5.
For the sequential estimation, we use (10) in (21) and (22), where the values of
the coefficients βs are the result of the estimation presented in Table 3. We have
again a mixture of logit models, but with fewer parameters, as the parameters of
the structural equation are not re-estimated. The specification file is presented in
Section B.5. The estimated parameters of the choice model are presented in
Table 6.
It is important to realize that the estimation results in Tables 5 and 6 cannot
be compared, as they are not using the same data.
Table 6: Estimation results for the sequential estimation
| | | | Robust | | | Parameter | | Coeff. | Asympt. | |
| number | Description | estimate | std. error | t-stat | p-value
|
|
|
|
|
|
|
|
|
|
| | 1 | ASC_CAR | 0. | 617 | 0. | 149 | 4. | 14 | 0. | 00 | | 2 |
ASC_SM | 0. | 0304 | 0. | 296 | 0. | 10 | 0. | 92 | | 3 |
BETA_COST_HWH | -1. | 79 | 0. | 534 | -3. | 35 | 0. | 00 | | 4 |
BETA_COST_OTHER | -1. | 20 | 0. | 849 | -1. | 41 | 0. | 16 | | 5 |
BETA_DIST | -1. | 42 | 0. | 360 | -3. | 93 | 0. | 00 | | 6 |
BETA_TIME_CAR_CL | -0. | 401 | 0. | 291 | -1. | 38 | 0. | 17 | | 7 |
BETA_TIME_CAR_REF | -13. | 5 | 4. | 25 | -3. | 17 | 0. | 00 | | 8 |
BETA_TIME_PT_CL | 0. | 662 | 1. | 05 | 0. | 63 | 0. | 53 | | 9 |
BETA_TIME_PT_REF | -3. | 15 | 2. | 02 | -1. | 56 | 0. | 12 | | 10 |
BETA_WAITING_TIME | -0. | 0519 | 0. | 0307 | -1. | 69 | 0. | 09 |
|
|
|
|
|
|
|
|
|
| | |
|
Summary statistics
| Number of observations = 1906 | Number of excluded observations = 359
| Number of estimated parameters = 10
| 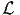 (β0) (β0) | = | -2093.955 |
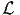 ( (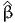 ) ) | = | -1174.054 |
-2[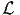 (β0) - (β0) - 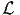 ( (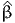 )] )] | = | 1839.802 |
| ρ2 | = | 0.439 |
| ρ2 | = | 0.435 |
| |
|
5 Full information estimation
The proper way of estimating the model is to jointly estimate the parameters of
the structural equation and the parameters of the choice model, using both the
indicators and the choice data.
As the latent variable, and therefore εs, is involved in both the measurement
equations for the indicators, and the measurement equations of the choice model,
the joint likelihood must be first calculated conditional on εs:
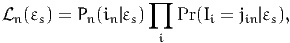 | (27) |
where in is the observed choice of individual n, and jin is the response of
individual n to the psychometric question i. The contribution to the likelihood of
this individual is then
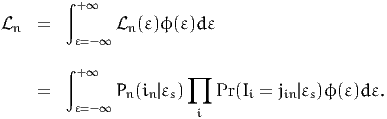 | (28) |
The specification file is provided in Section B.6, and the estimation results in
Tables 7 and 8.
Table 7: Estimation results for the full information estimation
| | | | Robust | |
| Parameter | | Coeff. | Asympt. | |
| number | Description | estimate | std. error | t-stat | p-value
|
|
|
|
|
|
|
|
|
|
|
| 1 | ASC_CAR | 0. | 703 | 0. | 118 | 5. | 96 | 0. | 00 |
| 2 |
ASC_SM | 0. | 261 | 0. | 345 | 0. | 76 | 0. | 45 |
| 3 |
BETA_COST_HWH | -1. | 43 | 0. | 341 | -4. | 19 | 0. | 00 |
| 4 |
BETA_COST_OTHER | -0. | 526 | 0. | 161 | -3. | 27 | 0. | 00 |
| 5 |
BETA_DIST | -1. | 41 | 0. | 386 | -3. | 66 | 0. | 00 |
| 6 |
BETA_TIME_CAR_CL | -0. | 956 | 0. | 169 | -5. | 65 | 0. | 00 |
| 7 |
BETA_TIME_CAR_REF | -9. | 50 | 1. | 94 | -4. | 90 | 0. | 00 |
| 8 |
BETA_TIME_PT_CL | -0. | 456 | 0. | 143 | -3. | 19 | 0. | 00 |
| 9 |
BETA_TIME_PT_REF | -3. | 22 | 0. | 838 | -3. | 84 | 0. | 00 |
| 10 | BETA_WAITING_TIME | -0. | 0205 | 0. | 00962 | -2. | 13 | 0. | 03 |
| 11 | B_Envir02_F1 | -0. | 459 | 0. | 0308 | -14. | 88 | 0. | 00 |
| 12 | B_Envir03_F1 | 0. | 484 | 0. | 0316 | 15. | 32 | 0. | 00 |
| 13 | B_Mobil11_F1 | 0. | 572 | 0. | 0419 | 13. | 65 | 0. | 00 |
| 14 | B_Mobil14_F1 | 0. | 575 | 0. | 0350 | 16. | 42 | 0. | 00 |
| 15 | B_Mobil16_F1 | 0. | 525 | 0. | 0425 | 12. | 36 | 0. | 00 |
| 16 | B_Mobil17_F1 | 0. | 514 | 0. | 0420 | 12. | 25 | 0. | 00 |
| 17 | INTER_Envir02 | 0. | 460 | 0. | 0308 | 14. | 92 | 0. | 00 |
| 18 | INTER_Envir03 | -0. | 367 | 0. | 0289 | -12. | 69 | 0. | 00 |
| 19 | INTER_Mobil11 | 0. | 418 | 0. | 0373 | 11. | 22 | 0. | 00 |
| 20 | INTER_Mobil14 | -0. | 173 | 0. | 0278 | -6. | 21 | 0. | 00 |
| 21 | INTER_Mobil16 | 0. | 148 | 0. | 0336 | 4. | 39 | 0. | 00 |
| 22 | INTER_Mobil17 | 0. | 140 | 0. | 0329 | 4. | 24 | 0. | 00 |
| |
Table 8: Estimation results for the full information estimation (ctd.)
| | | | Robust | | | Parameter | | Coeff. | Asympt. | |
| number | Description | estimate | std. error | t-stat | p-value
|
|
|
|
|
|
|
|
|
|
| | 23 | SIGMA_STAR_Envir02 | 0. | 918 | 0. | 0344 | 26. | 63 | 0. | 00 | | 24 |
SIGMA_STAR_Envir03 | 0. | 857 | 0. | 0352 | 24. | 34 | 0. | 00 | | 25 |
SIGMA_STAR_Mobil11 | 0. | 895 | 0. | 0409 | 21. | 89 | 0. | 00 | | 26 |
SIGMA_STAR_Mobil14 | 0. | 759 | 0. | 0333 | 22. | 81 | 0. | 00 | | 27 |
SIGMA_STAR_Mobil16 | 0. | 873 | 0. | 0397 | 21. | 97 | 0. | 00 | | 28 |
SIGMA_STAR_Mobil17 | 0. | 876 | 0. | 0392 | 22. | 36 | 0. | 00 | | 29 |
coef_ContIncome_0_4000 | 0. | 146 | 0. | 0606 | 2. | 41 | 0. | 02 | | 30 |
coef_ContIncome_10000_more | 0. | 119 | 0. | 0365 | 3. | 25 | 0. | 00 | | 31 |
coef_ContIncome_4000_6000 | -0. | 279 | 0. | 114 | -2. | 45 | 0. | 01 | | 32 |
coef_ContIncome_6000_8000 | 0. | 321 | 0. | 137 | 2. | 34 | 0. | 02 | | 33 |
coef_ContIncome_8000_10000 | -0. | 666 | 0. | 157 | -4. | 25 | 0. | 00 | | 34 |
coef_age_65_more | 0. | 0403 | 0. | 0748 | 0. | 54 | 0. | 59 |
| 35 | coef_haveChildren | -0. | 0276 | 0. | 0563 | -0. | 49 | 0. | 62 | | 36 |
coef_haveGA | -0. | 745 | 0. | 0999 | -7. | 46 | 0. | 00 | | 37 |
coef_highEducation | -0. | 266 | 0. | 0670 | -3. | 96 | 0. | 00 |
| 38 | coef_individualHouse | -0. | 116 | 0. | 0560 | -2. | 08 | 0. | 04 | | 39 |
coef_intercept | 0. | 373 | 0. | 169 | 2. | 21 | 0. | 03 |
| 40 | coef_male | 0. | 0776 | 0. | 0534 | 1. | 45 | 0. | 15 | | 41 |
coef_moreThanOneBike | -0. | 365 | 0. | 0686 | -5. | 32 | 0. | 00 | | 42 |
coef_moreThanOneCar | 0. | 711 | 0. | 0667 | 10. | 66 | 0. | 00 | | 43 |
delta_1 | 0. | 328 | 0. | 0127 | 25. | 81 | 0. | 00 | | 44 |
delta_2 | 0. | 989 | 0. | 0358 | 27. | 64 | 0. | 00 | | 45 |
sigma_s | 0. | 855 | 0. | 0549 | 15. | 57 | 0. | 00 |
|
|
|
|
|
|
|
|
|
| | |
|
Summary statistics
| Number of observations = 1906 | Number of excluded observations = 359
| Number of estimated parameters = 45
| 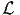 ( (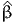 ) ) | = | -18383.063 |
| |
|
6 Serial correlation
The likelihood function (27)–(28) assumes that the error terms involved in the
models are independent, that is, εim in (13), and the errors terms of the utility
functions (20). However, because all these models apply to the same individual
who made the choice and provided the indicators, these error terms may
actually be correlated as they potentially share unobserved variables specific
to this individual. This issue, called serial correlation, can be handled
by including an agent effect in the model specification. This is an error
component appearing in all the models involved, distributed across the
individuals.
The specification file is provided in Section B.7, and the estimation results in
Tables 9 and 10. In our example, the parameter of the agent affect appears not to
be significant, with a p-value of 0.82. Note also that the integral is approximated
here using Monte-Carlo simulation.
Table 9: Estimation results for the full information estimation with agent
effect
| | | | Robust | | | Parameter | | Coeff. | Asympt. | |
| number | Description | estimate | std. error | t-stat | p-value
|
|
|
|
|
|
|
|
|
|
| | 1 | ASC_CAR | 0. | 703 | 0. | 118 | 5. | 95 | 0. | 00 | | 2 |
ASC_SM | 0. | 261 | 0. | 343 | 0. | 76 | 0. | 45 | | 3 |
BETA_COST_HWH | -1. | 43 | 0. | 340 | -4. | 21 | 0. | 00 | | 4 |
BETA_COST_OTHER | -0. | 525 | 0. | 161 | -3. | 27 | 0. | 00 | | 5 |
BETA_DIST | -1. | 41 | 0. | 383 | -3. | 69 | 0. | 00 | | 6 |
BETA_TIME_CAR_CL | -0. | 953 | 0. | 166 | -5. | 74 | 0. | 00 | | 7 |
BETA_TIME_CAR_REF | -9. | 50 | 1. | 93 | -4. | 91 | 0. | 00 | | 8 |
BETA_TIME_PT_CL | -0. | 454 | 0. | 136 | -3. | 35 | 0. | 00 | | 9 |
BETA_TIME_PT_REF | -3. | 22 | 0. | 838 | -3. | 85 | 0. | 00 | | 10 |
BETA_WAITING_TIME | -0. | 0204 | 0. | 00962 | -2. | 12 | 0. | 03 | | 11 |
B_Envir02_F1 | -0. | 459 | 0. | 0309 | -14. | 86 | 0. | 00 | | 12 |
B_Envir03_F1 | 0. | 484 | 0. | 0316 | 15. | 31 | 0. | 00 | | 13 |
B_Mobil11_F1 | 0. | 572 | 0. | 0420 | 13. | 62 | 0. | 00 | | 14 |
B_Mobil14_F1 | 0. | 575 | 0. | 0351 | 16. | 40 | 0. | 00 | | 15 |
B_Mobil16_F1 | 0. | 525 | 0. | 0426 | 12. | 34 | 0. | 00 | | 16 |
B_Mobil17_F1 | 0. | 514 | 0. | 0420 | 12. | 23 | 0. | 00 | | 17 |
INTER_Envir02 | 0. | 460 | 0. | 0308 | 14. | 92 | 0. | 00 | | 18 |
INTER_Envir03 | -0. | 367 | 0. | 0289 | -12. | 69 | 0. | 00 | | 19 |
INTER_Mobil11 | 0. | 418 | 0. | 0373 | 11. | 22 | 0. | 00 | | 20 |
INTER_Mobil14 | -0. | 173 | 0. | 0278 | -6. | 20 | 0. | 00 | | 21 |
INTER_Mobil16 | 0. | 147 | 0. | 0337 | 4. | 37 | 0. | 00 | | 22 |
INTER_Mobil17 | 0. | 140 | 0. | 0329 | 4. | 24 | 0. | 00 | | |
|
Table 10: Estimation results for the full information estimation with agent
effect (ctd.)
| | | | Robust | | | Parameter | | Coeff. | Asympt. | |
| number | Description | estimate | std. error | t-stat | p-value
|
|
|
|
|
|
|
|
|
|
| | 23 | SIGMA_STAR_Envir02 | 0. | 918 | 0. | 0345 | 26. | 63 | 0. | 00 | | 24 |
SIGMA_STAR_Envir03 | 0. | 857 | 0. | 0352 | 24. | 34 | 0. | 00 | | 25 |
SIGMA_STAR_Mobil11 | 0. | 895 | 0. | 0409 | 21. | 88 | 0. | 00 | | 26 |
SIGMA_STAR_Mobil14 | 0. | 760 | 0. | 0333 | 22. | 80 | 0. | 00 | | 27 |
SIGMA_STAR_Mobil16 | 0. | 873 | 0. | 0398 | 21. | 94 | 0. | 00 | | 28 |
SIGMA_STAR_Mobil17 | 0. | 877 | 0. | 0392 | 22. | 35 | 0. | 00 | | 29 |
coef_ContIncome_0_4000 | 0. | 147 | 0. | 0606 | 2. | 43 | 0. | 02 | | 30 |
coef_ContIncome_10000_more | 0. | 119 | 0. | 0364 | 3. | 26 | 0. | 00 | | 31 |
coef_ContIncome_4000_6000 | -0. | 281 | 0. | 114 | -2. | 47 | 0. | 01 | | 32 |
coef_ContIncome_6000_8000 | 0. | 322 | 0. | 137 | 2. | 34 | 0. | 02 | | 33 |
coef_ContIncome_8000_10000 | -0. | 666 | 0. | 157 | -4. | 25 | 0. | 00 | | 34 |
coef_age_65_more | 0. | 0411 | 0. | 0748 | 0. | 55 | 0. | 58 |
| 35 | coef_haveChildren | -0. | 0253 | 0. | 0566 | -0. | 45 | 0. | 66 | | 36 |
coef_haveGA | -0. | 743 | 0. | 0999 | -7. | 44 | 0. | 00 | | 37 |
coef_highEducation | -0. | 267 | 0. | 0669 | -3. | 99 | 0. | 00 |
| 38 | coef_individualHouse | -0. | 116 | 0. | 0560 | -2. | 08 | 0. | 04 | | 39 |
coef_intercept | 0. | 370 | 0. | 169 | 2. | 19 | 0. | 03 |
| 40 | coef_male | 0. | 0773 | 0. | 0534 | 1. | 45 | 0. | 15 | | 41 |
coef_moreThanOneBike | -0. | 366 | 0. | 0688 | -5. | 32 | 0. | 00 | | 42 |
coef_moreThanOneCar | 0. | 710 | 0. | 0668 | 10. | 63 | 0. | 00 | | 43 |
delta_1 | 0. | 328 | 0. | 0127 | 25. | 80 | 0. | 00 | | 44 |
delta_2 | 0. | 989 | 0. | 0358 | 27. | 62 | 0. | 00 | | 45 |
ec_sigma | -0. | 0178 | 0. | 0768 | -0. | 23 | 0. | 82 |
| 46 | sigma_s | 0. | 856 | 0. | 0551 | 15. | 55 | 0. | 00 |
|
|
|
|
|
|
|
|
|
| | |
|
Summary statistics
| Number of observations = 1906 | Number of excluded observations = 359
| Number of estimated parameters = 46
| 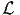 ( (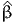 ) ) | = | -18383.598 |
| |
|
7 Discussions
We conclude with some comments this short introduction to the estimation of
choice models with latent variables.
- The initial values of the σ parameters involved in the model specification
should be large enough, and in any case certainly not 0. Indeed, if
they are too small, the likelihood of some observations may be so
small that they are numerically 0. Therefore, calculating the log
likelihood is impossible and the estimation will fail even before the first
iteration. in this case, PythonBiogeme produces the following message:
Init. log-likelihood: -1.79769e+308 [00:00] Warning: Error: There is a numerical problem with the initial log likelihood. It typically happens when one observation is associated with a very low probability, so that taking the log generates a very high number. Modify the starting values of the parameters. You may want to use the SIMULATE feature of pythonbiogeme to identify the cause of the problem.
- The sign of the σ parameters is irrelevant. It is perfectly fine to obtain a
negative number.
- As discussed above, the estimation of these models involve the calculation
of integrals that have no closed form. If there is only one random
variable to integrate, it is in general more efficient to use numerical
integration, using the Integrate tool of PythonBiogeme. If there are more,
Monte-Carlo integration should be preferred. We refer the reader
to Bierlaire (2015) for a detailed description of how to do it with
PythonBiogeme.
- It seems to be common practice to use linear regression on the indicators,
assuming that they are continuous variables, as described in Section 2.1. We
suggest to avoid that practice, and to prefer an ordered probit formulation
as described in Section 2.2, to account for the discrete nature of the
indicators. Also, ordered probit should be preferred to ordered logit, as the
latter is not based on a symmetric distribution.
- It is strongly advised to use the sequential estimation of the model during
the model development phase, as the estimation time is significantly
reduced. However, once the specification has been finalized, a full
information estimation of the parameters should be performed.
- The behavioral interpretation of the latent variable is relevant in the context
of the indicators that have been collected. When only the choice data are
used for the estimation, the interpretation of the latent variable is
meaningless as such. It is only relevant in the context of the choice model. It
can be seen that the estimates of the parameters using the indicators,
presented in Tables 1–2, 3–4 and 7–8 are completely different than
the estimates obtained using only the choice data, presented in
Table 5. As an example, we illustrate the variation of the latent
variable as a function of income in Figure 2, where it is seen that the
three estimates involving the indicators capture qualitatively the
same pattern, while the one with only the choice data is completely
different.
- We refer the reader to Vij and Walker (2016), who discuss the actual added
value (or lack thereof) of using latent variables in the context of a choice
model.
A Description of the case study
This case study deals with the estimation of a mode choice behavior model for
inhabitants in Switzerland using revealed preference data. The survey was
conducted between 2009 and 2010 for CarPostal, the public transport branch of
the Swiss Postal Service. The main purpose of this survey is to collect
data for analyzing the travel behavior of people in low-density areas,
where CarPostal typically serves. A following study proposes new public
transport alternatives according to the respondents’ willingness to pay for
these potential services in order to increase the market share of public
transport.
A.1 Data collection
The survey covers French and German speaking areas of Switzerland.
Questionnaires were sent to people living in rural area by mail. The respondents
were asked to register all the trips performed during a specified day. The collected
information consists of origin, destination, cost, travel time, chosen mode and
activity at the destination. Moreover, we collected socio-economic information
about the respondents and their households.
1124 completed surveys were collected. For each respondent, cyclic sequences
of trips (starting and ending at the same location) are detected and their main
transport mode is identified. The resulting data base includes 1906 sequences of
trips linked with psychometric indicators and socio-economic attributes of the
respondents. It should be noticed that each observation is a sequence of trips that
starts and ends at home. A respondent may have several sequences of trips in a
day.
A.2 Variables and descriptive statistics
The variables are described in Table 11. The attitudinal statements are described
in Table 12. A summary of descriptive statistics for the main variables is given in
Table 13.
Given the presence of missing data (coded as -1) an additional table
summarizing the three main affected variables (TripPurpose, ReportedDuration,
age) after removing the missing cases is presented (see Table 14).
| |
|
|
| Table 11: Description of variables
|
|
|
|
Name |
Description |
|
|
|
ID |
Identifier of the respondent who described the trips
in the loop. |
|
|
|
NbTransf |
The total number of transfers performed for all
trips of the loop, using public transport (ranging
from 1-9). |
|
|
|
TimePT |
The duration of the loop performed in public
transport (in minutes). |
|
|
|
WalkingTimePT |
The total walking time in a loop performed in
public transports (in minutes). |
|
|
|
WaitingTimePT |
The total waiting time in a loop performed in
public transports (in minutes). |
|
|
|
TimeCar |
The total duration of a loop made using the car
(in minutes). |
|
|
|
CostPT |
Cost for public transports (full cost to perform the
loop). |
|
|
|
MarginalCostPT |
The total cost of a loop performed in public
transports, taking into account the ownership
of a seasonal ticket by the respondent. If the
respondent has a “GA” (full Swiss season ticket), a
seasonal ticket for the line or the area, this variable
takes value zero. If the respondent has a half-fare
travelcard, this variable corresponds to half the
cost of the trip by public transport.. |
|
|
|
CostCarCHF |
The total gas cost of a loop performed with the
car in CHF. |
|
|
|
CostCar |
The total gas cost of a loop performed with the
car in euros. |
|
|
|
TripPurpose |
The main purpose of the loop: 1 =Work-related
trips; 2 =Work- and leisure-related trips; 3
=Leisure related trips. -1 represents missing values |
|
|
|
TypeCommune |
The commune type, based on the Swiss Federal
Statistical Office 1 =Centers; 2 =Suburban
communes; 3 =High-income communes; 4
=Periurban communes; 5 =Touristic communes; 6
=Industrial and tertiary communes; 7 =Rural and
commuting communes; 8 =Agricultural and mixed
communes; 9 =Agricultural communes |
|
|
|
UrbRur |
Binary variable, where: 1 =Rural; 2 =Urban. |
|
|
|
ClassifCodeLine |
Classification of the type of bus lines of
the commune: 1 =Center; 2 =Centripetal; 3
=Peripheral; 4 =Feeder. |
|
|
|
frequency |
Categorical variable for the frequency: 1 =Low
frequency, < 12 pairs of trips per day; 2
=Low-middle frequency, 13 - 20 pairs of trips per
day; 3 =Middle-high frequency, 21-30 pairs of trips
per day; 4 =High frequency, > 30 pairs of trips per
day. |
|
|
|
NbTrajects |
Number of trips in the loop |
|
|
|
Region OR
CoderegionCAR |
Region where the commune of the respondent is
situated. These regions are defined by CarPostal
as follows: 1 =Vaud; 2 =Valais; 3 =Delemont; 4
=Bern; 5 =Basel, Aargau, Olten; 6 =Zurich; 7
=Eastern Switzerland; 8 =Graubunden. |
|
|
|
distance_km |
Total distance performed for the loop. |
| | |
|
|
|
Choice |
Choice variable: 0 = public transports (train, bus,
tram, etc.); 1 = private modes (car, motorbike,
etc.); 2 = soft modes (bike, walk, etc.). |
|
|
|
InVehicleTime |
Time spent in (on-board) the transport modes
only (discarding walking time and waiting time),
-1 if missing value. |
|
|
|
ReportedDuration |
Time spent for the whole loop, as reported by the
respondent. -1 represents missing values |
|
|
|
LangCode |
Language of the commune where the survey was
conducted: 1 =French; 2 =German. |
|
|
|
age |
Age of the respondent (in years) -1 represents
missing values. |
|
|
|
DestAct |
The main activity at destination: 1 is work, 2 is
professional trip, 3 is studying, 4 is shopping, 5 is
activity at home, 6 is eating/drinking, 7 is personal
business, 8 is driving someone, 9 is cultural activity
or sport, 10 is going out (with friends, restaurant,
cinema, theater), 11 is other and -1 is missing
value. |
|
|
|
FreqTripHouseh |
Frequency of trips related to the household (drive
someone, like kids, or shopping), 1 is never, 2 is
several times a day, 3 is several times a week, 4
is occasionally, -1 is for missing data and -2 if
respondent didn’t answer to any opinion questions. |
|
ModeToSchool |
Most often mode used by the respondent to go to
school as a kid (> 10), 1 is car (passenger), 2 is
train, 3 is public transport, 4 is walking, 5 is biking,
6 is motorbike, 7 is other, 8 is multiple modes, -1 is
for missing data and -2 if respondent didn’t answer
to any opinion questions. |
|
|
|
ResidChild |
Main place of residence as a kid (< 18), 1 is city
center (large town), 2 is city center (small town),
3 is suburbs, 4 is suburban town, 5 is country
side (village), 6 is countryside (isolated), -1 is for
missing data and -2 if respondent didn’t answer to
any opinion questions. |
|
|
|
FreqCarPar |
Frequency of the usage of car by the respondent’s
parents (or adults in charge) during childhood
(< 18), 1 is never, 2 is occasionally, 3 is regularly,
4 is exclusively, -1 is for missing data and -2 if
respondent didn’t answer to any opinion questions. |
|
|
|
FreqTrainPar |
Frequency of the usage of train by the respondent’s
parents (or adults in charge) during childhood
(< 18), 1 is never, 2 is occasionally, 3 is regularly,
4 is exclusively, -1 is for missing data and -2 if
respondent didn’t answer to any opinion questions. |
|
|
|
FreqOthPar |
Frequency of the usage of tram, bus and other
public transport (not train) by the respondent’s
parents (or adults in charge) during childhood
(< 18), 1 is never, 2 is occasionally, 3 is regularly,
4 is exclusively , -1 is for missing data and -2 if
respondent didn’t answer to any opinion questions. |
|
|
|
NbHousehold |
Number of persons in the household. -1 for missing
value. |
|
|
|
NbChild |
Number of kids (< 15) in the household. -1 for
missing value. |
|
|
|
NbCar |
Number of cars in the household.-1 for missing
value. |
|
|
|
NbMoto |
Number of motorbikes in the household. -1 for
missing value. |
|
|
|
NbBicy |
Number of bikes in the household. -1 for missing
value. |
|
|
|
NbBicyChild |
Number of bikes for kids in the household. -1 for
missing value. |
|
|
|
NbComp |
Number of computers in the household. -1 for
missing value. |
|
|
|
NbTV |
Number of TVs in the household. -1 for missing
value. |
|
|
|
|
|
Internet |
Internet connection, 1 is yes, 2 is no. -1 for missing
value. |
|
|
|
NewsPaperSubs |
Newspaper subscription, 1 is yes, 2 is no. -1 for
missing value. |
|
|
|
NbCellPhones |
Number of cell phones in the household (total). -1
for missing value. |
|
|
|
NbSmartPhone |
Number of smartphones in the household (total).
-1 for missing value. |
|
|
|
HouseType |
House type, 1 is individual house (or terraced
house), 2 is apartment (and other types of
multi-family residential), 3 is independent room
(subletting). -1 for missing value. |
|
|
|
OwnHouse |
Do you own the place where you are living? 1 is
yes, 2 is no. -1 for missing value. |
|
|
|
NbRoomsHouse |
Number of rooms is your house. -1 for missing
value. |
|
|
|
YearsInHouse |
Number of years spent in the current house. -1 for
missing value. |
|
|
|
Income |
Net monthly income of the household in CHF. 1
is less than 2500, 2 is from 2501 to 4000, 3 is from
4001 to 6000, 4 is from 6001 to 8000, 5 is from 8001
to 10’000 and 6 is more than 10’001. -1 for missing
value. |
|
|
|
Gender |
Gender of the respondent, 1 is man, 2 is woman.
-1 for missing value. |
|
|
|
BirthYear |
Year of birth of the respondent. -1 for missing
value. |
|
|
|
Mothertongue |
Mothertongue. 1 for German or Swiss German, 2
for french, 3 for other, -1 for missing value. |
|
|
|
FamilSitu |
Familiar situation: 1 is single, 2 is in a couple
without children, 3 is in a couple with children, 4 is
single with your own children, 5 is in a colocation,
6 is with your parents and 7 is for other situations.
-1 for missing values. |
|
|
|
OccupStat |
What is you occupational status? 1 is for full-time
paid professional activity, 2 for partial-time paid
professional activity, 3 for searching a job, 4 for
occasional employment, 5 for no paid job, 6 for
homemaker, 7 for disability leave, 8 for student and
9 for retired. -1 for missing values. |
|
|
|
SocioProfCat |
To which of the following socio-professional
categories do you belong? 1 is for top managers,
2 for intellectual professions, 3 for freelancers, 4
for intermediate professions, 5 for artisans and
salespersons, 6 for employees, 7 for workers and 8
for others. -1 for missing values. |
|
|
|
Education |
Highest education achieved. As mentioned by
Wikipedia in English: ”The education system
in Switzerland is very diverse, because the
constitution of Switzerland delegates the authority
for the school system mainly to the cantons. The
Swiss constitution sets the foundations, namely
that primary school is obligatory for every child
and is free in public schools and that the
confederation can run or support universities.”
(source:
http://en.wikipedia.org/wiki/Education_in_Switzerland,
accessed April 16, 2013). It is thus difficult
to translate the survey that was originally in
French and German. The possible answers in the
survey are: 1. Unfinished compulsory education:
education is compulsory in Switzerland but pupils
may finish it at the legal age without succeeding
the final exam. 2. Compulsory education with
diploma 3. Vocational education: a three or
four-year period of training both in a company
and following theoretical courses. Ends with a
diploma called ”Certificat fédéral de capacité”
(i.e., ”professional baccalaureate”) 4. A 3-year
generalist school giving access to teaching school,
nursing schools, social work school, universities
of applied sciences or vocational education
(sometime in less than the normal number of
years). It does not give access to universities in
Switzerland 5. High school: ends with the general
baccalaureate exam. The general baccalaureate
gives access automatically to universities. 6.
Universities of applied sciences, teaching schools,
nursing schools, social work schools: ends with a
Bachelor and sometimes a Master, mostly focus on
vocational training 7. Universities and institutes of
technology: ends with an academic Bachelor and
in most cases an academic Master 8. PhD thesis |
|
|
|
HalfFareST |
Is equal to 1 if the respondent has a half-fare
travelcard and to 2 if not. |
|
|
|
LineRelST |
Is equal to 1 if the respondent has a line-related
season ticket and 2 if not. |
|
|
|
GenAbST |
Is equal to 1 if the respondent has a GA (full Swiss
season ticket) and 2 if not. |
|
|
|
AreaRelST |
Is equal to 1 if the respondent has an area-related
season ticket and 2 if not. |
|
|
|
|
|
OtherST |
Is equal to 1 if the respondent has a season ticket
that was is not in the list and 2 if not. |
|
|
|
CarAvail |
Represents the availability of a car for the
respondent: 1 is always, 2 is sometime, 3 is never.
-1 for missing value. |
|
|
| |
| |
|
|
|
|
|
|
| |
|
|
| Table 12: Attitude questions. Coding: 1= strongly disagree, 2=disagree, 3=neutral,
4= agree, 5= strongly agree, 6=not applicable, -1= missing value, -2= all answers to
attitude questions missing
|
|
|
|
Name |
Description |
|
|
|
Envir01 |
Fuel price should be increased to reduce congestion
and air pollution. |
|
|
|
Envir02 |
More public transportation is needed, even if taxes
are set to pay the additional costs. |
|
|
|
Envir03 |
Ecology disadvantages minorities and small
businesses. |
|
|
|
Envir04 |
People and employment are more important than
the environment. |
|
|
|
Envir05 |
I am concerned about global warming. |
|
|
|
Envir06 |
Actions and decision making are needed to limit
greenhouse gas emissions. |
|
|
|
Mobil01 |
My trip is a useful transition between home and
work. |
|
|
|
Mobil02 |
The trip I must do interferes with other things I
would like to do. |
|
|
|
Mobil03 |
I use the time of my trip in a productive way. |
|
|
|
Mobil04 |
Being stuck in traffic bores me. |
|
|
|
Mobil05 |
I reconsider frequently my mode choice. |
|
|
|
Mobil06 |
I use my current mean of transport mode because
I have no alternative. |
|
|
|
Mobil07 |
In general, for my activities, I always have a usual
mean of transport. |
|
|
|
Mobil08 |
I do not feel comfortable when I travel close to
people I do not know. |
|
|
|
Mobil09 |
Taking the bus helps making the city more
comfortable and welcoming. |
|
|
|
Mobil10 |
It is difficult to take the public transport when I
travel with my children. |
|
|
|
Mobil11 |
It is difficult to take the public transport when I
carry bags or luggage. |
|
|
|
Mobil12 |
It is very important to have a beautiful car. |
| |
|
|
|
|
Mobil13 |
With my car I can go wherever and whenever. |
|
|
|
Mobil14 |
When I take the car I know I will be on time. |
|
|
|
Mobil15 |
I do not like looking for a parking place. |
|
|
|
Mobil16 |
I do not like changing the mean of transport when
I am traveling. |
|
|
|
Mobil17 |
If I use public transportation I have to cancel
certain activities I would have done if I had taken
the car. |
|
|
|
Mobil18 |
CarPostal bus schedules are sometimes difficult to
understand. |
|
|
|
Mobil19 |
I know very well which bus/train I have to take to
go where I want to. |
|
|
|
Mobil20 |
I know by heart the schedules of the public
transports I regularly use. |
|
|
|
Mobil21 |
I can rely on my family to drive me if needed |
|
|
|
Mobil22 |
When I am in a town I don’t know I feel strongly
disoriented |
|
|
|
Mobil23 |
I use the internet to check the schedules and the
departure times of buses and trains. |
|
|
|
Mobil24 |
I have always used public transports all my life |
|
|
|
Mobil25 |
When I was young my parents took me to all my
activities |
|
|
|
Mobil26 |
I know some drivers of the public transports that
I use |
|
|
|
Mobil27 |
I think it is important to have the option to talk
to the drivers of public transports. |
|
|
|
ResidCh01 |
I like living in a neighborhood where a lot of things
happen. |
|
|
|
ResidCh02 |
The accessibility and mobility conditions are
important for the choice of housing. |
|
|
|
ResidCh03 |
Most of my friends live in the same region I live
in. |
|
|
|
ResidCh04 |
I would like to have access to more services or
activities. |
|
|
|
ResidCh05 |
I would like to live in the city center of a big city. |
|
|
|
|
|
ResidCh06 |
I would like to live in a town situated in the
outskirts of a city. |
|
|
|
ResidCh07 |
I would like to live in the countryside. |
|
|
|
LifSty01 |
I always choose the best products regardless of
price. |
|
|
|
LifSty02 |
I always try to find the cheapest alternative. |
|
|
|
LifSty03 |
I can ask for services in my neighborhood without
problems. |
|
|
|
LifSty04 |
I would like to spend more time with my family
and friends. |
|
|
|
LifSty05 |
Sometimes I would like to take a day off . |
|
|
|
LifSty06 |
I can recognize the social status of other travelers
by looking at their cars. |
|
|
|
LifSty07 |
The pleasure of having something beautiful
consists in showing it. |
|
|
|
LifSty08 |
For me the car is only a practical way to move. |
|
|
|
LifSty09 |
I would like to spend more time working. |
|
|
|
LifSty10 |
I do not like to be in the same place for too long. |
|
|
|
LifSty11 |
I always plan my activities well in advance |
|
|
|
LifSty12 |
I like to experiment new or different situations |
|
|
|
LifSty13 |
I am not afraid of unknown people |
|
|
|
LifSty14 |
My schedule is rather regular. |
|
|
| |
| |
|
|
|
|
|
|
Table 13: Descriptive statistics of the main variables (no data excluded)
|
|
|
|
|
|
|
|
| | nbr. cases | nbr. null | min | max | median | mean | std.dev |
|
|
|
|
|
|
|
|
| age | 1906 | 0 | -1 | 88 | 47 | 46.48 | 18.57 |
|
|
|
|
|
|
|
|
| Choice | 1906 | 536 | 0 | 2 | 1 | 0.78 | 0.54 |
|
|
|
|
|
|
|
|
| TypeCommune | 1906 | 0 | 1 | 9 | 6 | 5.39 | 1.99 |
|
|
|
|
|
|
|
|
| UrbRur | 1906 | 0 | 1 | 2 | 2 | 1.51 | 0.5 |
|
|
|
|
|
|
|
|
| ClassifCodeLine | 1906 | 0 | 1 | 4 | 4 | 3.17 | 0.97 |
|
|
|
|
|
|
|
|
| LangCode | 1906 | 0 | 1 | 2 | 2 | 1.74 | 0.44 |
|
|
|
|
|
|
|
|
| CoderegionCAR | 1906 | 0 | 1 | 8 | 5 | 4.58 | 2.08 |
|
|
|
|
|
|
|
|
| CostCarCHF | 1906 | 5 | 0 | 67.65 | 2.98 | 5.76 | 8.34 |
|
|
|
|
|
|
|
|
| distance_km | 1906 | 1 | 0 | 519 | 18.75 | 40.38 | 62.6 |
|
|
|
|
|
|
|
|
| TimeCar | 1906 | 28 | 0 | 494 | 26 | 40.68 | 47.61 |
|
|
|
|
|
|
|
|
| TimePT | 1906 | 7 | 0 | 745 | 85 | 107.88 | 86.52 |
|
|
|
|
|
|
|
|
| frequency | 1906 | 0 | 1 | 4 | 3 | 2.84 | 1.09 |
|
|
|
|
|
|
|
|
| ID | 1906 | 0 | 10350017 | 96040538 | 44690042 | 45878800 | 23846908 |
|
|
|
|
|
|
|
|
| InVehicleTime | 1906 | 66 | -128 | 631 | 40.5 | 55.13 | 57.78 |
|
|
|
|
|
|
|
|
| MarginalCostPT | 1906 | 270 | 0 | 230 | 5.6 | 11.11 | 16.13 |
|
|
|
|
|
|
|
|
| NbTrajects | 1906 | 0 | 1 | 9 | 2 | 2.04 | 1.05 |
|
|
|
|
|
|
|
|
| NbTransf | 1906 | 644 | 0 | 14 | 2 | 2.01 | 2.17 |
|
|
|
|
|
|
|
|
| Region | 1906 | 0 | 1 | 8 | 5 | 4.58 | 2.08 |
|
|
|
|
|
|
|
|
| ReportedDuration | 1906 | 3 | -1 | 855 | 35 | 57.73 | 72.47 |
|
|
|
|
|
|
|
|
| TripPurpose | 1906 | 0 | -1 | 3 | 2 | 1.94 | 1.18 |
|
|
|
|
|
|
|
|
| WaitingTimePT | 1906 | 693 | 0 | 392 | 5 | 13.13 | 22.07 |
|
|
|
|
|
|
|
|
| WalkingTimePT | 1906 | 17 | 0 | 213 | 33 | 39.63 | 28 |
|
|
|
|
|
|
|
|
| |
Table 14: Descriptive statistics of the main variables affected by missing
data (observations with -1 excluded)
|
|
|
|
|
|
|
|
| | nbr. cases | nbr.null | min | max | median | mean | std.dev |
|
|
|
|
|
|
|
|
| age | 1791 | 0 | 16 | 88 | 48 | 49.53 | 14.59 |
|
|
|
|
|
|
|
|
| ReportedDuration | 1835 | 3 | 0 | 855 | 37 | 60 | 72.92 |
|
|
|
|
|
|
|
|
| TripPurpose | 1783 | 0 | 1 | 3 | 3 | 2.14 | 0.92 |
|
|
|
|
|
|
|
|
| |
B Complete specification files
B.1 factoranalysis.r
B.2 01oneLatentRegression.py
B.3 02oneLatentOrdered.py
B.4 03choiceOnly.py
B.5 04latentChoiceSeq.py
B.6 05latentChoiceFull.py
B.7 06serialCorrelation.py
References
Ashok, K., Dillon, W. R. and Yuan, S. (2002). Extending discrete
choice models to incorporate attitudinal and other latent variables,
Journal of Marketing Research 39(1): 31–46.
Atasoy, B., Glerum, A. and Bierlaire, M. (2011). Mode choice with
attitudinal latent class: a swiss case-study, Proceedings of the Second
International Choice Modeling Conference, Leeds, UK.
Atasoy, B., Glerum, A. and Bierlaire, M. (2013). Attitudes towards
mode choice in switzerland, disP - The Planning Review 49(2): 101–117.
Ben-Akiva, M., Walker, J., Bernardino, A. T., Gopinath, D. A.,
Morikawa, T. and Polydoropoulou, A. (2002). Integration of choice
and latent variable models, Perpetual motion: Travel behaviour research
opportunities and application challenges pp. 431–470.
Bierlaire, M. (2015). Monte-carlo integration with pythonbiogeme,
Technical Report 150806, Transport and Mobility Laboratory, Ecole
Polytechnique Fédérale de Lausanne.
Greene, W. H. and Hensher, D. A. (2003). A latent class model
for discrete choice analysis: contrasts with mixed logit, Transportation
Research Part B: Methodological 37(8): 681–698.
Likert, R. (1932). A technique for the measurement of attitudes,
Archives of psychology 140: 1–55.
Vij, A. and Walker, J. L. (2016). How, when and why integrated choice
and latent variable models are latently useful, Transportation Research
Part B: Methodological 90: 192–217.
Walker, J. L. (2001). Extended discrete choice models: integrated
framework, flexible error structures, and latent variables, PhD thesis,
Massachusetts Institute of Technology.
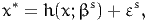
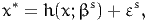
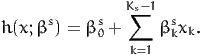
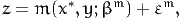
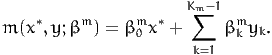
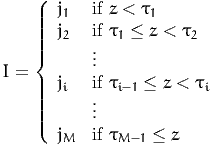
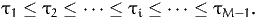
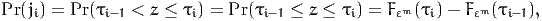
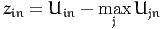
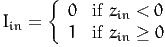
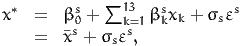
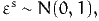
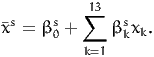
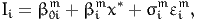
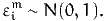
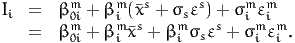
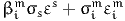
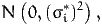
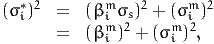
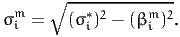
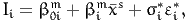
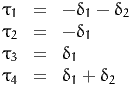
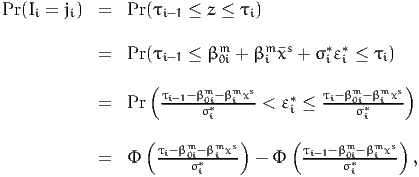
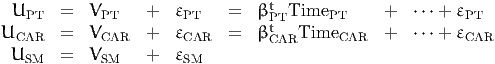
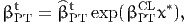
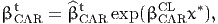
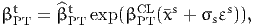
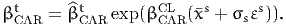
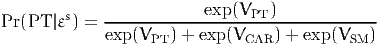
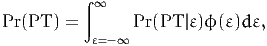
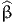 tPT in (21),
tPT in (21),
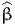 tCAR in (22).
tCAR in (22).